Which Multiple Comparison Test to Use After Anova?
Introduction
Suppose that we fit a one-way ANOVA model to a data. Let ![]() be the number of treatment levels. Hence the fitted ANOVA model equation is given by
be the number of treatment levels. Hence the fitted ANOVA model equation is given by ![]() where
where ![]() and
and ![]() . Multiple comparison tests are used to find confidence intervals for a combination of contrasts or treatment means, given a required simultaneous confidence level. For example, we would like to find confidence intervals for the contrasts
. Multiple comparison tests are used to find confidence intervals for a combination of contrasts or treatment means, given a required simultaneous confidence level. For example, we would like to find confidence intervals for the contrasts ![]() and
and ![]() and the probability that these two intervals are both true is 95%, that is, the simultaneous confidence level is 95%.
and the probability that these two intervals are both true is 95%, that is, the simultaneous confidence level is 95%.
We are going to consider five multiple comparison test methods, each of them have their own particular use. Each method will be described in more details below.

Recall that a contrast is a linear combination of the ![]() ‘s:
‘s: ![]() where each
where each ![]() such that
such that ![]() . For example,
. For example, ![]() is a contrast because it can be written in the form
is a contrast because it can be written in the form ![]() where
where ![]() ,
, ![]() and
and ![]() otherwise. The confidence interval of
otherwise. The confidence interval of ![]() gives us the confidence interval for the difference between the effects of treatment levels 1 and 2.
gives us the confidence interval for the difference between the effects of treatment levels 1 and 2.
Bonferroni Method
The Bonferroni Method is used only for pre-planned contrasts and means. This means that we would know the list of contrasts for which to find their confidence interval, before looking at the results of the data or before performing the ANOVA test. Thus we are not using the data and its results to help us identity the contrasts or means for which to compute the confidence interval.
Recall that the ![]() % two-tailed confidence level for a contrast
% two-tailed confidence level for a contrast ![]() is given by:
is given by:
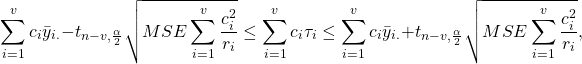
where ![]() is the mean response of the subjects assigned treatment level
is the mean response of the subjects assigned treatment level ![]() ,
, ![]() is the sample size,
is the sample size, ![]() is the Mean Square Error found from the data by computing
is the Mean Square Error found from the data by computing ![]() and
and ![]() is percentile of the
is percentile of the ![]() -distribution with
-distribution with ![]() degrees of freedom corresponding to a right-tail probability of
degrees of freedom corresponding to a right-tail probability of ![]() .
.
Bonferroni’s method is based on the general probability result that for any collection of sets ![]() ,
, ![]() . Suppose that we have
. Suppose that we have ![]() such intervals, and we would like that such intervals are significantly correct with probability
such intervals, and we would like that such intervals are significantly correct with probability ![]() . Assume that each individual interval is correct with probability
. Assume that each individual interval is correct with probability ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} & \ \ \mathbb{P}[\mbox{all }m\mbox{ intervals are correct}]\\ &=1-\mathbb{P}[\mbox{at least one of the }m\mbox{ intervals is incorrect}]\\ &=1-\mathbb{P}[\bigcup_{j=1}^{m}\mbox{interval }j\mbox{ is incorrect} ]\\ &\geq 1-\sum_{j=1}^m\mathbb{P}[\mbox{interval }j\mbox{ is incorrect} ]\\ &= 1-\sum_{j=1}^m \beta\\ &=1-m \beta \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-86b08c8f4fcf08f3ac145cee10c65669_l3.png)
Let ![]() , that is,
, that is, ![]() . Hence having
. Hence having ![]() confidence intervals each having a confidence level of
confidence intervals each having a confidence level of ![]() ensures a simultaneous confidence level of at least
ensures a simultaneous confidence level of at least ![]() . Each individual confidence interval for a contrast is thus given by:
. Each individual confidence interval for a contrast is thus given by:
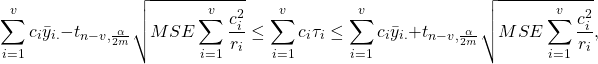
Note that in the trivial case when ![]() , the Bonferroni intervals are the same as the individual interval. When
, the Bonferroni intervals are the same as the individual interval. When ![]() , the simultaneous confidence intervals with combined
, the simultaneous confidence intervals with combined ![]() signifincance level are obviously wider than the individual confidence intervals with individual
signifincance level are obviously wider than the individual confidence intervals with individual ![]() signifincance level.
signifincance level.
Scheffe’s Method
Suppose that we compute the mean of each treatment level and possibly perform a one-way ANOVA. We would get an idea of the difference in effects (or lack of it) from the treatment levels. This would help us determine which contrasts are interesting for our study and for which we would like to find their confidence interval. Here we call such comparisons “Informed Comparisons” because the data is helping us choose the contrasts of interest. In this case, we should opt for Scheffe’s Method instead of Bonferroni’s Method. In contrast to the Bonferroni intervals, the Scheffe intervals do not depend on the number of intervals ![]() . This is based on the fact that any contrast can be written as a linear combination of the (treatment-control) contrasts:
. This is based on the fact that any contrast can be written as a linear combination of the (treatment-control) contrasts: ![]() . In fact:
. In fact:
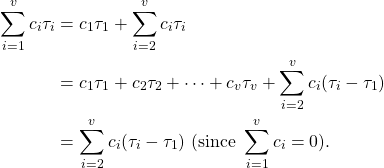
The Scheffe confidence intervals for contrasts giving a simultaneous confidence level of ![]() is given by:
is given by:
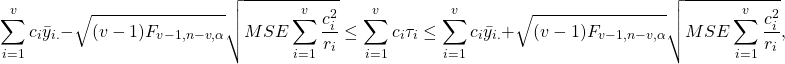
where ![]() is the percentile value of the
is the percentile value of the ![]() -distribution with
-distribution with ![]() and
and ![]() and right-tail probability of
and right-tail probability of ![]() .
.
Tukey’s Method
Tukey’s Method is used in order to find confidence intervals for all pairwise mean comparisons. Thus we will be finding ![]() confidence intervals for the following contrasts:
confidence intervals for the following contrasts: ![]() . Note that Tukey’s method provides narrower intervals than Bonferroni’s or Scheffe’s Method when considering exactly all the pairwise comparisons. Hence in such case Tukey’s Method should preferred.
. Note that Tukey’s method provides narrower intervals than Bonferroni’s or Scheffe’s Method when considering exactly all the pairwise comparisons. Hence in such case Tukey’s Method should preferred.
The Tukey confidence interval for contrast ![]() where
where ![]() that gives a simultaneous confidence level of at least
that gives a simultaneous confidence level of at least ![]() is given by:
is given by:
![]()
where ![]() is the percentile of the Studentized range distribution with parameters
is the percentile of the Studentized range distribution with parameters ![]() (number of groups) and
(number of groups) and ![]() (degrees of freedom), corresponding to a right-tail probability of
(degrees of freedom), corresponding to a right-tail probability of ![]() .
.
Dunnett’s Method
Suppose that we have one of the treatment levels which has a particular significance to the study. This is labelled as the “control”. For example, in practise the control could be a placebo, whereas the remaining treatments are different versions of drug developed by a pharmaceutical company. Dunnett’s Method is used to compare the control to all of the other treatments. W.l.o.g. let us say that the control is the first treatment level. Hence in Dunnett’s method we find ![]() confidence levels for the contrasts:
confidence levels for the contrasts: ![]() . The confidence intervals found by Dunnett’s Method are narrower than those provided by Bonferroni’s, Scheffe’s or Tukey’s method, in the case of treatment-control contrasts. Hence in such case Dunnett’s Method is preferred. The confidence intervals in this method are based on the multivariate
. The confidence intervals found by Dunnett’s Method are narrower than those provided by Bonferroni’s, Scheffe’s or Tukey’s method, in the case of treatment-control contrasts. Hence in such case Dunnett’s Method is preferred. The confidence intervals in this method are based on the multivariate ![]() -distribution. The Dunnett confidence interval for contrast
-distribution. The Dunnett confidence interval for contrast ![]() giving a simultaneous confidence level of
giving a simultaneous confidence level of ![]() is given by:
is given by:
![]()
where ![]() is the upper critical value for the maximum of the absolute values of a multivariate
is the upper critical value for the maximum of the absolute values of a multivariate ![]() -distribution with correlation 0.5 and
-distribution with correlation 0.5 and ![]() error degrees of freedom, corresponding to a right-tail probability of
error degrees of freedom, corresponding to a right-tail probability of ![]() .
.
Hsu’s Method
In Hsu’s method, ![]() confidence intervals are computed corresponding to a comparison between each treatment with the best of the other treatments (the treatment with the highest mean). If the resultant confidence interval is positive (contains no negative values), then the treatment is declared as the best treatment. If the resultant confidence interval is negative (contains no positive values), then the treatment is declared as not the best treatment. For equal treatment level sizes
confidence intervals are computed corresponding to a comparison between each treatment with the best of the other treatments (the treatment with the highest mean). If the resultant confidence interval is positive (contains no negative values), then the treatment is declared as the best treatment. If the resultant confidence interval is negative (contains no positive values), then the treatment is declared as not the best treatment. For equal treatment level sizes ![]() , the confidence interval which gives a simultaneous confidence level of
, the confidence interval which gives a simultaneous confidence level of ![]() , corresponding to the comparison between treatment
, corresponding to the comparison between treatment ![]() and the best of the other treatments, is given by:
and the best of the other treatments, is given by:
![]()
where ![]() is the precentile of the maximum of a multivariate
is the precentile of the maximum of a multivariate ![]() -distribution with correlation 0.5 and
-distribution with correlation 0.5 and ![]() degrees of freedom corresponding to a right-tail probability of
degrees of freedom corresponding to a right-tail probability of ![]() .
.
References
Design and Analysis of Experiments by Dean, Voss and Draguljic