HOme Loan Prepayment Calculator
Interest Rate
Original Duration
Monthly Repayment
Interest Paid:
Month of First Prepayment
New Monthly Repayment
Actual Duration
Actual Interest Paid:
How to use the Home Loan Prepayment Calculator
The calculator accepts the following as its inputs:
1) The Principal (![]() ) which is the loan amount.
) which is the loan amount.
2) The Interest Rate (![]() ) which is the nominal interest rate compounded monthly.
) which is the nominal interest rate compounded monthly.
3) The Original Duration (![]() ) which is the original duration of the loan in months. This results in
) which is the original duration of the loan in months. This results in ![]() equal monthly repayments that repay the loan in full after exactly
equal monthly repayments that repay the loan in full after exactly ![]() months.
months.
The “Monthly Repayment & Interest Paid” button, calculates the monthly repayment ![]() and total interest paid on the loan given that no prepayment is present.
and total interest paid on the loan given that no prepayment is present.
The calculator accepts a further two inputs that define the prepayment structure of the loan:
4) The Month of First Prepayment (![]() ) is the month from which the repayments are increased from
) is the month from which the repayments are increased from ![]() to a constant value
to a constant value ![]() . Note that
. Note that ![]() is an integer between 1 and
is an integer between 1 and ![]() .
.
5) The New Monthly Repayment (![]() ) is the repayment amount that is going to be paid monthly from month
) is the repayment amount that is going to be paid monthly from month ![]() onwards in order to prepay the loan. Note that
onwards in order to prepay the loan. Note that ![]() must be greater than
must be greater than ![]() in order to result in prepayments and thus an early repayment of the loan.
in order to result in prepayments and thus an early repayment of the loan.
The “Actual Duration & Interest Paid” button, calculates the duration ![]() in months given that prepayment is present and also the actual interest paid given that prepayment is made as defined by the inputs
in months given that prepayment is present and also the actual interest paid given that prepayment is made as defined by the inputs ![]() and
and ![]() .
.
Example: Suppose that we have a loan of amount €100,000 with a nominal interest rate of 3% compounded monthly that will be repaid in full in 20 years. Thus the first set of inputs for the calculator are ![]() ,
, ![]() and
and ![]() . When we click the “Monthly Repayment & Interest Paid” button, we obtain 554.60 for the Monthly Repayment and 33103.42 for the Interest Paid. This means that according to the repayment schedule, if we pay €554.60 per month, we will be able to repay such a loan in exactly 20 years (that is, 240 months). Moreover, we will paying a total interest of €33,103.42 over the whole duration of the loan.
. When we click the “Monthly Repayment & Interest Paid” button, we obtain 554.60 for the Monthly Repayment and 33103.42 for the Interest Paid. This means that according to the repayment schedule, if we pay €554.60 per month, we will be able to repay such a loan in exactly 20 years (that is, 240 months). Moreover, we will paying a total interest of €33,103.42 over the whole duration of the loan.
Suppose that we are going to start the prepayments from the sixth year of the loan, where the monthly repayment is going to be €700 instead of the usual €554.60. Thus the second set of inputs consists of ![]() and
and ![]() . When we click the “Actual Duration” button, we obtain 212. This means that at month 212 (that is, in
. When we click the “Actual Duration” button, we obtain 212. This means that at month 212 (that is, in ![]() years), the loan will be repaid in full.
years), the loan will be repaid in full.
Mathematical Derivation of the Monthly Repayment & Interest Paid
Consider a loan which has an associated principal amount ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and term
compounded monthly and term ![]() months. The borrower pays back
months. The borrower pays back ![]() equal monthly payments of amount
equal monthly payments of amount ![]() each, in order to redeem the loan. The loan repayments can be visualised with the help of a timeline:
each, in order to redeem the loan. The loan repayments can be visualised with the help of a timeline:
 The source code for drawing Timeline diagrams with ‘ggplot2’ in R is available here
The source code for drawing Timeline diagrams with ‘ggplot2’ in R is available here
The principal ![]() is the present value of the
is the present value of the ![]() repayment each of amount
repayment each of amount ![]() , using the interest rate of
, using the interest rate of ![]() . Thus:
. Thus:
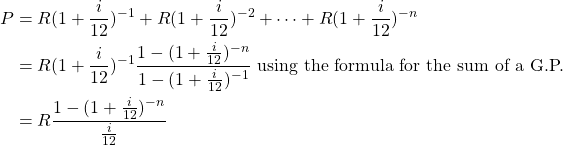
By making ![]() subject of the formula, we can see that the repayment amount
subject of the formula, we can see that the repayment amount ![]() can be calculated from
can be calculated from ![]() ,
, ![]() and
and ![]() by using the equation:
by using the equation:
![]()
The total interest paid is the sum of the total repayments made to the bank over the duration of the loan minus the principal amount ![]() . This is calculated by the equation:
. This is calculated by the equation:
![]()
Mathematical Derivation of the Actual Duration
Now suppose that from the ![]() repayment onwards, the repayment amount becomes
repayment onwards, the repayment amount becomes ![]() instead of
instead of ![]() where
where ![]() and
and ![]() . In the case when
. In the case when ![]() , the prepayments starts from the first payment, that is the end of the first month. In the case where
, the prepayments starts from the first payment, that is the end of the first month. In the case where ![]() , the prepayment starts from the last payment, which results in no prepayment, because the loan would have either way be closed with that last payment.
, the prepayment starts from the last payment, which results in no prepayment, because the loan would have either way be closed with that last payment.
The following time line shows the repayments of the loan when prepayment is present. The variable ![]() describes the new duration of the loan in months, given that prepayment is present.
describes the new duration of the loan in months, given that prepayment is present.

The loan amount ![]() is thus the present value of
is thus the present value of ![]() payments each of amount
payments each of amount ![]() and
and ![]() payments of
payments of ![]() , and thus we obtain the following equation:
, and thus we obtain the following equation:
![]() .
.
Using the theory related to geometic progressions, the equation is simplified as:
![]()
Making ![]() subject of the formula, we get:
subject of the formula, we get:
![]()
Since ![]() must be an integer, the duration of the loan in months given that the prepayment starts from month
must be an integer, the duration of the loan in months given that the prepayment starts from month ![]() , is given by:
, is given by:
![]()
Mathematical Derivation of the Actual Interest Paid
Let us consider the prepayment starting at month ![]() , where the monthly repayment increases from
, where the monthly repayment increases from ![]() to
to ![]() . At time
. At time ![]() , we do not know the exact repayment amount that would close off the loan. Let us denote the repayment amount at time
, we do not know the exact repayment amount that would close off the loan. Let us denote the repayment amount at time ![]() by
by ![]() . The value of
. The value of ![]() could lie anywhere in the range
could lie anywhere in the range ![]() . Hence the loan, given that prepayments are present could be represented by the following timeline:
. Hence the loan, given that prepayments are present could be represented by the following timeline:

Thus, the principal ![]() is the present value of
is the present value of ![]() payments of size
payments of size ![]() ,
, ![]() payments of size
payments of size ![]() and one payment of size
and one payment of size ![]() . So we obtain the following equation:
. So we obtain the following equation:
![]()
When the equation is simplified and ![]() is made subject of the formula, we can deduce the size of the last payment made at time
is made subject of the formula, we can deduce the size of the last payment made at time ![]() :
:
![]()
The actual interest paid is the sum of all the repayments minus the principal, given by the formula:
![]()