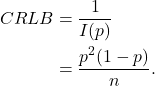The Cramer Rao Lower Bound for the Geometric Distribution

The Cramer Rao Lower Bound for The Geometric Distribution

Introduction

Suppose that we have a unbiased estimator of a parameter of a distribution. The Cramer-Rao inequality provides us with a lower bound for the variance of such an estimator. After we compute the Cramer-Rao Lower Bound (CRLB), we can check whether the unbiased estimator at hand reaches a minimum variance over all the unbiased estimators of the parameter.

The following is the Cramer-Rao Inequality.

Let $\hat{\theta}$ be an unbiased estimator of $\theta$ which is a parameter of the distribution with probability density function $f(x;\theta)$ and log-likelihood $l(x;\theta)=\ln f(x;\theta)$ . Then the Cramer-Rao Inequality is given by:

$\begin{equation*}var(\hat{\theta})\geq\frac{1}{I(\theta)}\end{equation*}$

where the function $I(\theta)$ known as Fisher Information is given by $I(\theta)=-n\mathbb{E}\Big[\frac{\delta^2 l(x;\theta)}{\delta \theta^2}\Big]$ , and $n$ is the sample size over which the estimator $\hat{\theta}$ is estimated.

Thus the Cramer-Rao Lower Bound for the variance of $\hat{\theta}$ is given by: $\frac{1}{I(\theta)}$ , that is, $\frac{1}{-n\mathbb{E}\big[\frac{\delta^2 l(x;\theta)}{\delta \theta^2}\Big]}$ .

In this article, we will derive the Cramer-Rao Lower Bound of an estimator of the parameter $p$ of the geometric distribution.

The Geometric Distribution

The probability density function of the geometric distribution (having parameter $p$ ) is given by:

$\begin{equation*}f(x;p)=(1-p)^{x-1}p\text{ for }x=1,2,3,\cdots\end{equation*}$

Using standard probability theory, it follows that for the geometric distribution $\mathbb{E}[x]=\frac{1}{p}$ .

The Cramer-Rao Lower Bound for the Geometric Distribution

Consider first the Fisher Information for the Geometric Distribution with parameter $p$ .

$\begin{equation*}\begin{align}I(p)&=-n\mathbb{E}\Big[\frac{\delta^2 l(x;p)}{\delta p^2}\Big]\\ &=-n\mathbb{E}\Big[\frac{\delta^2}{\delta p^2} [\ln ((1-p)^{x-1}p)]\Big]\\ &=-n\mathbb{E}\Big[\frac{\delta^2}{\delta p^2} [(x-1)\ln (1-p)+\ln p]\Big]\\ &=-n\mathbb{E}\Big[\frac{\delta}{\delta p} [-\frac{x-1}{1-p}+\frac{1}{p}]\Big]\\ &=n\mathbb{E}\Big[\frac{\delta}{\delta p} [\frac{x-1}{1-p}-\frac{1}{p}]\Big]\\ &=n\mathbb{E}\Big[\frac{x-1}{(1-p)^2}+\frac{1}{p^2}\Big]\\ &=n\Big(\frac{\mathbb{E}[x]-1}{(1-p)^2}+\frac{1}{p^2}\Big)\\ &=n\Big(\frac{\frac{1}{p}-1}{(1-p)^2}+\frac{1}{p^2}\Big)\text{ (since }\mathbb{E}[x]=\frac{1}{p})\\ &=n\Big(\frac{1-p}{p(1-p)^2}+\frac{1}{p^2}\Big)\\ &=n\Big(\frac{1}{p(1-p)}+\frac{1}{p^2}\Big)\\ &=n\Big(\frac{p+(1-p)}{p^2(1-p)} \Big)\\ &=\frac{n}{p^2(1-p)}. \end{align} \end{equation*}$

Thus, the Cramer-Rao Lower Bound for the variance of an estimator of $p$ of the geometric distribution is given by:

$\begin{equation*} \begin{align} CRLB&=\frac{1}{I(p)}\\ &=\frac{p^2(1-p)}{n}. \end{align} \end{equation*}$