The Effect of Loan Prepayment on THe Balance Sheet
Introduction
We study the various effects of prepayment on a loan arising from two scenarios. We consider loans that are repaid by a sequence of fixed monthly instalments over a pre-stated number of months. The first scenario is that when the monthly repayment amount is increase by some fixed factor from some month onwards. The second scenario is that when there is a decrease in the interest rate during the lifetime of the loan, whilst the repayment amount is kept constant instead of revised downwards.
We define the prepayment rate based on the expected and the actual monthly outstanding principal, and in both instances we provide closed formulae for the actual duration of the loan and the monthly prepayment rate for each month, in terms of the loan parameters. Moreover we consider the interest income lost at each month due to the underlying prepayment.
The theory is extended to analyse the effects of prepayment on a portfolio of loans. The portfolio prepayment rate is computed together with the actual outstanding combined portfolio principal. This is an exercise for the asset-liability management of the lending institution. Together with the analysis of the future actual portfolio interest income inflow, all of this could be useful in the risk assessment of the loan portfolio.
The structure of the document is as follows. First we consider the repayment schedule of a loan, which provides the repayment structure of the loan given that prepayment is not present. Then scenario one in presented. We consider the case when prepayment starts immediately from the first month. Then this is extended to the general case in which the prepayment can start at any predetermined month. Finally the theory is extended to analyse a portfolio of loans. The second scenario is presented in a similar fashion.
The Repayment Schedule
Consider a loan which has an associated principal amount ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and term
compounded monthly and term ![]() months. The borrower pays back
months. The borrower pays back ![]() equal monthly payments of amount
equal monthly payments of amount ![]() each, in order to redeem the loan. In fact, the repayment schedule which includes each monthly repayment broken down into the interest and capital component, and the monthly outstanding principal, can be computed from just the knowledge of
each, in order to redeem the loan. In fact, the repayment schedule which includes each monthly repayment broken down into the interest and capital component, and the monthly outstanding principal, can be computed from just the knowledge of ![]() ,
, ![]() and
and ![]() . In other words
. In other words ![]() ,
, ![]() and
and ![]() define such a loan completely.
define such a loan completely.
The repayment amount ![]() can be calculated from
can be calculated from ![]() ,
, ![]() and
and ![]() by using the equation:
by using the equation:
(1) 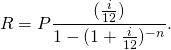
This follows from the fact that ![]() is the present value of
is the present value of ![]() payments each of amount
payments each of amount ![]() each, using a discounting rate of
each, using a discounting rate of ![]() . It can be shown by induction that the interest component, the capital component and outstanding principal at month
. It can be shown by induction that the interest component, the capital component and outstanding principal at month ![]() can be described in terms of
can be described in terms of ![]() ,
, ![]() ,
, ![]() and
and ![]() as follows:
as follows:
Lemma 1: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the monthly repayment as calculated in equation (1). The interest and capital component in the
be the monthly repayment as calculated in equation (1). The interest and capital component in the ![]() repayment and the outstanding principal at month
repayment and the outstanding principal at month ![]() , for
, for ![]() , are given by:
, are given by:

From Lemma 1 we can obtain the proportion of the ![]() payment that corresponds to interest payment and the proportion that corresponds to the repayment of capital. These are obtained by the dividing the formulae for
payment that corresponds to interest payment and the proportion that corresponds to the repayment of capital. These are obtained by the dividing the formulae for ![]() and
and ![]() by
by ![]() .
.
Lemma 2: The proportions of the interest and capital component in the ![]() repayment for
repayment for ![]() , are given by:
, are given by:

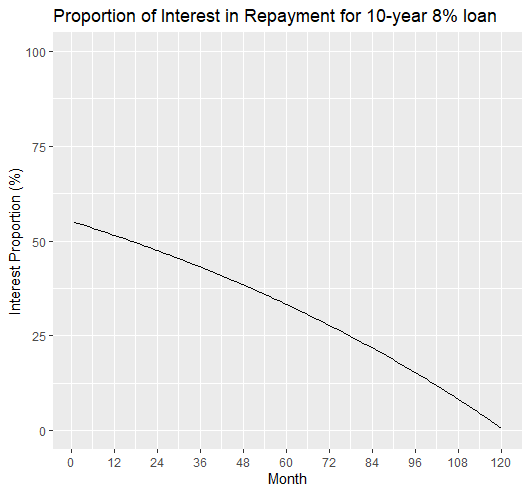
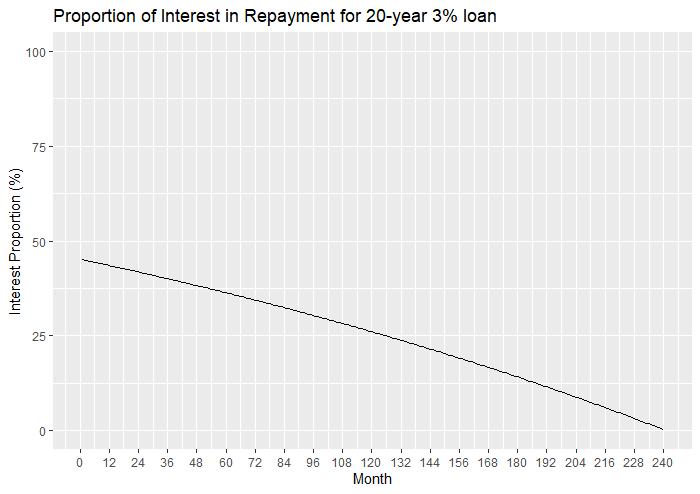
We see that these proportions do not depend on the loan principal ![]() . These depend on the term of the loan and the interest rate, and the payment number
. These depend on the term of the loan and the interest rate, and the payment number ![]() of the loan. The following two plots show the proportion of interest in the repayments over the life of a loan. We consider two examples. The first one is a 10-year loan (
of the loan. The following two plots show the proportion of interest in the repayments over the life of a loan. We consider two examples. The first one is a 10-year loan (![]() ) with an interest rate of 8% and the second one is a 20-year loan (
) with an interest rate of 8% and the second one is a 20-year loan (![]() ) with an interest rate of 3%. Note that these plots also show the proportion of capital in the repayments, because
) with an interest rate of 3%. Note that these plots also show the proportion of capital in the repayments, because ![]() for all
for all ![]() . Thus we can see the decrease (or increase respectively) of the interest proportion (or capital proportion) with
. Thus we can see the decrease (or increase respectively) of the interest proportion (or capital proportion) with ![]() .
.
The sum of the capital components of all the ![]() repayments is equal to
repayments is equal to ![]() , the loan principal. The total interest paid on the loan is:
, the loan principal. The total interest paid on the loan is:
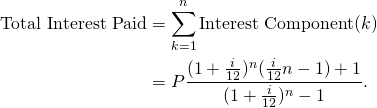
The proportion of the total interest paid over the Principal amount ![]() is independent of
is independent of ![]() and depends only on
and depends only on ![]() and
and ![]() .
.
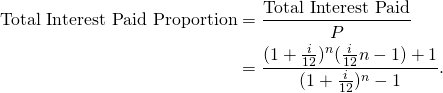
Constant Prepayment from Month 1
There are instances in which the borrower makes one or more monthly repayments that are greater than the value ![]() as determined by the repayment schedule. This results in what is known prepayment or early repayment of a loan. The prepayment rate of a loan at month
as determined by the repayment schedule. This results in what is known prepayment or early repayment of a loan. The prepayment rate of a loan at month ![]() is defined as the extra capital repaid until month
is defined as the extra capital repaid until month ![]() divided by the outstanding principal according to the repayment schedule at month
divided by the outstanding principal according to the repayment schedule at month ![]() . This is given by the equation:
. This is given by the equation:
(2) ![]()
where ![]() ,
, ![]() stands for the outstanding principal according to the repayment schedule at month
stands for the outstanding principal according to the repayment schedule at month ![]() and
and ![]() stands for the actual outstanding principal at month
stands for the actual outstanding principal at month ![]() .
.
Suppose we have a loan in which the borrower increases each monthly repayment by a factor of ![]() , that is, each repayment is
, that is, each repayment is ![]() instead of the value
instead of the value ![]() as stated by the repayment schedule. We are after: (1) the prepayment rate at each month (2) the actual duration of the loan. First, from Lemma 1 we can deduce the capital, interest component and outstanding principal in this instance.
as stated by the repayment schedule. We are after: (1) the prepayment rate at each month (2) the actual duration of the loan. First, from Lemma 1 we can deduce the capital, interest component and outstanding principal in this instance.
Lemma 3: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the actual repayment amount where the value
be the actual repayment amount where the value ![]() as calculated in equation (1). Let
as calculated in equation (1). Let ![]() be the actual duration of the loan, given that prepayment is present. The interest and capital component in the
be the actual duration of the loan, given that prepayment is present. The interest and capital component in the ![]() repayment and the outstanding principal at month
repayment and the outstanding principal at month ![]() , for
, for ![]() are given by:
are given by:
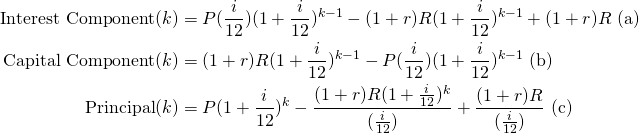
Proof: By induction on ![]() .
. ![]()
Result 1: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. When the actual monthly repayment is increased by a factor of
months. When the actual monthly repayment is increased by a factor of ![]() , the prepayment rate at month
, the prepayment rate at month ![]() , for
, for ![]() , is:
, is:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Prepayment Rate}(k)=\frac{r[(1+\frac{i}{12})^k-1]}{1-(1+\frac{i}{12})^{k-n}}.\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-35ac676598dbd1b10d9261490e3266e9_l3.png)
Proof:
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\text{Prepayment Rate}(k)&= \frac{\text{Principal}_{\text{RS}}(k)-\text{Principal}_{\text{Actual}}(k)}{\text{Principal}_{\text{RS}}(k)} \text{ (by Equation 2})\\&=\frac{P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}-P(1+\frac{i}{12})^k+\frac{(1+r)R(1+\frac{i}{12})^k}{(\frac{i}{12})}-\frac{(1+r)R}{(\frac{i}{12})}}{P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}}\text{ (by Lemma 1(c)and Lemma 3(c))}\\&=\frac{\frac{rR(1+\frac{i}{12})^k}{(\frac{i}{12})}-\frac{rR}{(\frac{i}{12})}}{P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}}\\&=\frac{\frac{rR(1+\frac{i}{12})^k}{(\frac{i}{12})}-\frac{rR}{(\frac{i}{12})}}{\frac{R}{(\frac{i}{12})}(1-(1+\frac{i}{12})^{-n})(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}} \text{ (by Equation 1})\\&=\frac{r(1+\frac{i}{12})^k-r}{(1-(1+\frac{i}{12})^{-n})(1+\frac{i}{12})^k-(1+\frac{i}{12})^k+1}\\&=\frac{r[(1+\frac{i}{12})^k-1]}{1-(1+\frac{i}{12})^{k-n}}.\mbox{ } \square\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-f5a5cca504bdb6ffeeb5334e735117da_l3.png)
Result 2: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. When the actual monthly repayment is increased by a factor of
months. When the actual monthly repayment is increased by a factor of ![]() , the actual duration of the loan is:
, the actual duration of the loan is:
![Rendered by QuickLaTeX.com \begin{equation*}\lceil \frac{\ln{(1+r)}-\ln{[r+(1+\frac{i}{12})^{-n}]}}{\ln{(1+\frac{i}{12})}} \rceil\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-c2a3b40439870cbbbd3dc1b6862c1080_l3.png)
Proof: Let ![]() be the least integer such that the prepayment rate is greater or equal to 1. Then
be the least integer such that the prepayment rate is greater or equal to 1. Then ![]() is the actual duration of the loan. Note that we assume that
is the actual duration of the loan. Note that we assume that ![]() and hence
and hence ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\text{Prepayment Rate}(k)&\geq 1\\\frac{r[(1+\frac{i}{12})^k-1]}{1-(1+\frac{i}{12})^{k-n}} &\geq 1\text{ (by Result 1})\\r(1+\frac{i}{12})^k-r &\geq 1-(1+\frac{i}{12})^{k-n}\\r(1+\frac{i}{12})^k+(1+\frac{i}{12})^{k-n} &\geq 1+r\\(1+\frac{i}{12})^k[r+(1+\frac{i}{12})^{-n}] &\geq 1+r\\(1+\frac{i}{12})^k&\geq\frac{1+r}{r+(1+\frac{i}{12})^{-n}}\\\ln{(1+\frac{i}{12})^k}&\geq \ln{\frac{1+r}{r+(1+\frac{i}{12})^{-n}}}\\k&\geq \frac{\ln{(1+r)}-\ln{(r+(1+\frac{i}{12})^{-n})}}{\ln{(1+\frac{i}{12})}}.\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-8bd4cef101e6c1dabb8904824a938b24_l3.png)
Hence result follows.
Note that Results 1 and 2 are independent of the principal ![]() . Note also that in the trivial case when
. Note also that in the trivial case when ![]() , the actual duration
, the actual duration ![]() is equal to the initial duration
is equal to the initial duration ![]() . At month
. At month ![]() , the loan is paid in full, and hence the prepayment rate at month
, the loan is paid in full, and hence the prepayment rate at month ![]() is equal to 1. In fact, at month
is equal to 1. In fact, at month ![]() , we have:
, we have:

Adding the ![]() interest and capital component gives us the
interest and capital component gives us the ![]() repayment amount:
repayment amount:
![]()
This is the last repayment amount which is smaller or equal to ![]() that closes off the loan.
that closes off the loan.
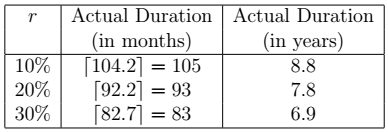
Let us consider some examples of loans and different scenarios of ![]() . We calculate the actual duration of the loan and plot prepayment rate curves which display the prepayment rates at different time points. Consider a loan with an interest rate of
. We calculate the actual duration of the loan and plot prepayment rate curves which display the prepayment rates at different time points. Consider a loan with an interest rate of ![]() and an initial duration of 10 years (
and an initial duration of 10 years (![]() ). We consider three values of
). We consider three values of ![]() : 10%, 20% and 30%. The next table gives the actual duration (using Result 2) of the loan given a particular value of
: 10%, 20% and 30%. The next table gives the actual duration (using Result 2) of the loan given a particular value of ![]() .
.
 values
valuesThe next figure shows the prepayment curves for the 10-year 8% loan when ![]() takes on values 10%, 20% and 30%.
takes on values 10%, 20% and 30%.

Prepayment curve of a 10-year 8% loan
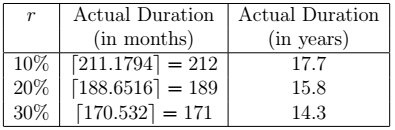
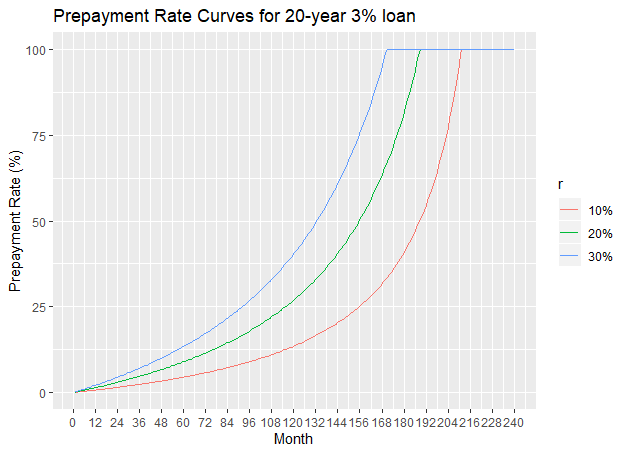
Consider a loan with an interest rate of 3% and an initial duration of 20 years (![]() ). We consider three values of
). We consider three values of ![]() : 10%, 20% and 30%. The next table gives the actual duration of this loan for the different values of
: 10%, 20% and 30%. The next table gives the actual duration of this loan for the different values of ![]() and the next figure shows the prepayment curves.
and the next figure shows the prepayment curves.
 values
values
The increase in the repayment results in a faster rate of decrease in the outstanding principal. Hence the lender will actually receive less interest than initially expected. We can compare the Interest Component![]() when prepayment is and is not present in order to calculate the reduction (loss) of interest income at each month
when prepayment is and is not present in order to calculate the reduction (loss) of interest income at each month ![]() for
for ![]() . We shall call the reducing in the interest at month
. We shall call the reducing in the interest at month ![]() : Interest Loss
: Interest Loss![]() and given by formula:
and given by formula:
![]()
where ![]() is the expected interest income at month
is the expected interest income at month ![]() according to the repayment schedule, and
according to the repayment schedule, and ![]() is the actual interest income receive at month
is the actual interest income receive at month ![]() when prepayment is present.
when prepayment is present.
Result 3: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the actual repayment amount where the value
be the actual repayment amount where the value ![]() as calculated in equation (1). The loss of interest in the
as calculated in equation (1). The loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss}(k)=\begin{cases}rR[(1+\frac{i}{12})^{k-1}-1], & \textup{for }1\leq k \leq z\\R[1-(1+\frac{i}{12})^{k-n-1}], & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-4413ca1aa7f9b780c7eeed9f552f7fd9_l3.png)
Proof: Let ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Interest Loss}(k)&=\textup{Interest Component}_{RS}(k)-\textup{Interest Component}_{Prep.}(k)\\&=[P(\frac{i}{12})(1+\frac{i}{12})^{k-1}-R(1+\frac{i}{12})^{k-1}+R]\\&\ \ \ -[P(\frac{i}{12})(1+\frac{i}{12})^{k-1}-(1+r)R(1+\frac{i}{12})^{k-1}+(1+r)R]\textup{ (by Lemmas 1(a) and 3a))}\\&=rR[(1+\frac{i}{12})^{k-1}-1].\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-5c47f79bd7c4a86b030084ac321654ef_l3.png)
Let ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Interest Loss}(k)&=\textup{Interest Component}_{RS}(k)-\textup{Interest Component}_{Prep.}(k)\\&=[ P(\frac{i}{12})(1+\frac{i}{12})^{k-1}-R(1+\frac{i}{12})^{k-1}+R]-0 \textup{ (by Lemma 1(a))}\\&=R[1-(1+\frac{i}{12})^{-n}](1+\frac{i}{12})^{k-1}-R(1+\frac{i}{12})^{k-1}+R \textup{ (by Equation 1)}\\&=R[1-(1+\frac{i}{12})^{k-n-1}].\ \ \ \square\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-26c58e8f3f09499713ef9a0079a62db2_l3.png)
We can consider the fraction of the interest loss from the expected amount of interest receivable. We shall call this the Interest Loss Percentage, which is independent of the principal amount ![]() . The Interest Loss Percentage at the
. The Interest Loss Percentage at the ![]() month is given by formula:
month is given by formula:

The values ![]() can be expressed as a function of the loan parameters as follows.
can be expressed as a function of the loan parameters as follows.
Result 4: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the actual repayment amount where the value
be the actual repayment amount where the value ![]() as calculated in Equation (1). The percentage of loss of interest in the
as calculated in Equation (1). The percentage of loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss Percentage}(k)=\begin{cases}\frac{r[(1+\frac{i}{12})^{k-1}-1]}{1-(1+\frac{i}{12})^{k-n-1}}\times 100\%, & \textup{for }1\leq k \leq z\\100\%, & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-a60425e7c514034749ac6d9d433e9fa8_l3.png)
The next figures show the plots of Interest Loss Percentage for two loans: a 10-year 8% loan and a 20-year 3% loan. The curves all start at a value of 0% at month 1. Then they increase to 100% at time ![]() when the loan is repaid in full prematurely.
when the loan is repaid in full prematurely.
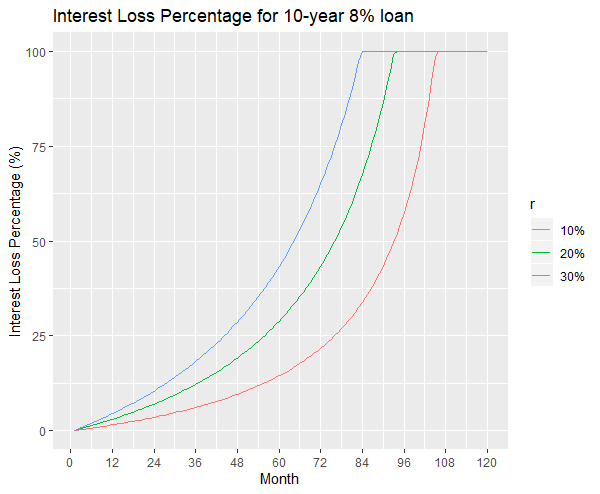
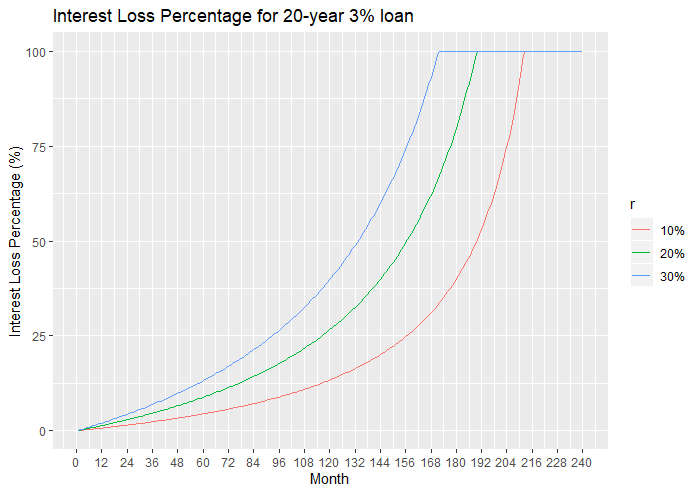
Let us consider the total interest paid on the loan in the case of having prepayments starting from the first month.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \textup{Total Interest Paid}&=\sum_{k=1}^{z} \textup{Interest Component}(k)\\ &=\frac{P}{1-(1+\frac{i}{12})^{-n}}[(r+(1+\frac{i}{12})^{-n})(1-(1+\frac{i}{12})^z)+(1+r)(\frac{i}{12}) z]. \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-dde806bc4697ccccba93583e35e9cea6_l3.png)
The fraction of the Total Interest Paid over the Principal amount is thus given by:
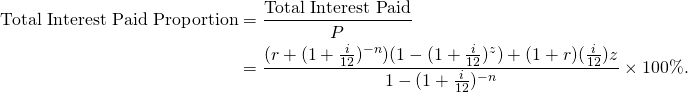
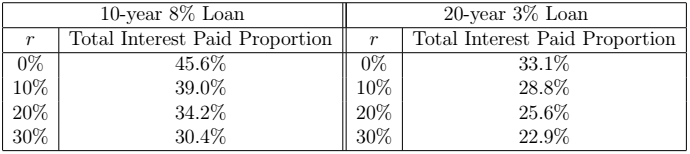
The next table gives the Total Interest Paid Proportion for the 10-year 8% loan and the 20-year 3% loan, for different values of ![]() . Note that
. Note that ![]() =0% is the case when there is no prepayment present. The total interest paid proportion is inversely related to
=0% is the case when there is no prepayment present. The total interest paid proportion is inversely related to ![]() .
.
We can also calculate the Total Interest Loss which is the total interest which is lost on a loan due to prepayments. This can be calculated in two ways: either by summing all the values of ![]() for
for ![]() or else by deducting the sum of the interest components when prepayment is present from the sum of interest components when prepayment is not present.
or else by deducting the sum of the interest components when prepayment is present from the sum of interest components when prepayment is not present.

The Total Interest Loss on an loan whose prepayments start in the first month is given by:
![]()
The Total Interest Loss Proportion is thus given by:
![]()
The next Table gives the Total Interest Loss Proportion for the 10-year 8% loan and the 20-year 3% loan, for different values of ![]() .
.

Constant Prepayment from Month 
Suppose now that the prepayments start from month ![]() , that is, the monthly repayment is
, that is, the monthly repayment is ![]() till month
till month ![]() and increases to
and increases to ![]() from month
from month ![]() onwards. The interest and capital components from the
onwards. The interest and capital components from the ![]() month repayment onwards change as follows.
month repayment onwards change as follows.
Lemma 4: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the amount repaid monthly until month
be the amount repaid monthly until month ![]() , as calculated in equation (1). Let
, as calculated in equation (1). Let ![]() be the monthly repayment amount from month
be the monthly repayment amount from month ![]() onwards. Let
onwards. Let ![]() be the actual duration of the loan, given that prepayment is present. The interest and capital component in the
be the actual duration of the loan, given that prepayment is present. The interest and capital component in the ![]() repayment and the outstanding principal at month
repayment and the outstanding principal at month ![]() , for
, for ![]() are given by:
are given by:
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Interest Component}(k) &= P(\frac{i}{12})(1+\frac{i}{12})^{k-1}-R(1+\frac{i}{12})^{k-1}+R+rR[1-(1+\frac{i}{12})^{k-m}] \textup{ (a)}\\\textup{Capital Component}(k) &= R(1+\frac{i}{12})^{k-1}-P(\frac{i}{12})(1+\frac{i}{12})^{k-1}+rR(1+\frac{i}{12})^{k-m} \textup{ (b)}\\\textup{Principal}(k)&=P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}+\frac{rR[1-(1+\frac{i}{12})^{k-m+1}]}{(\frac{i}{12})} \textup{ (c)}\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-1007aecf86d3a1f82733256e06856893_l3.png)
Proof: By induction on ![]() .
. ![]()
The next result gives the prepayment rate at each month.
Result 3: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the amount repaid monthly until month
be the amount repaid monthly until month ![]() , as calculated in equation (1). Let
, as calculated in equation (1). Let ![]() be the monthly repayment amount from month
be the monthly repayment amount from month ![]() onwards. Let
onwards. Let ![]() be the actual duration of the loan, given that prepayment is present. The prepayment rate at month
be the actual duration of the loan, given that prepayment is present. The prepayment rate at month ![]() for
for ![]() is 0, whilst the prepayment rate at month
is 0, whilst the prepayment rate at month ![]() for
for ![]() is:
is:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Prepayment Rate}(k)=\frac{r[(1+\frac{i}{12})^{k-m+1}-1]}{1-(1+\frac{i}{12})^{k-n}}.\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-9e4ea314a0256e83d12de5dd221fab99_l3.png)
Proof: The proof is similar to that of Result 1. ![]()
Note that Result 1 can now be viewed as a corollary of Result 3 obtained by fixing ![]() to be 1. The next result gives a formula for the actual duration
to be 1. The next result gives a formula for the actual duration ![]() of a loan.
of a loan.
Result 4: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. When the actual monthly repayment is increased by a factor of
months. When the actual monthly repayment is increased by a factor of ![]() from month
from month ![]() onwards, the actual duration of the loan is:
onwards, the actual duration of the loan is:
![Rendered by QuickLaTeX.com \begin{equation*}\lceil \frac{\ln{(1+r)}-\ln{[r(1+\frac{i}{12})^{1-m}+(1+\frac{i}{12})^{-n}]}}{\ln{(1+\frac{i}{12})}} \rceil\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-10126c62e96c32e62050b2ef45348bda_l3.png)
Proof: The proof is similar to that of Result 2. ![]()
At month ![]() , the loan is paid in full, and hence the prepayment rate at month
, the loan is paid in full, and hence the prepayment rate at month ![]() is equal to 1. In fact, at month
is equal to 1. In fact, at month ![]() , we have:
, we have:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \textup{Interest Component}(z) &=P(\frac{i}{12})(1+\frac{i}{12})^{z-1}-R(1+\frac{i}{12})^{z-1}+R+rR[1-(1+\frac{i}{12})^{z-m}] \\ \textup{Capital Component}(z) &=\textup{Principal}(z-1)=P(1+\frac{i}{12})^{z-1}-\frac{R(1+\frac{i}{12})^{z-1}}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}+\frac{rR[1-(1+\frac{i}{12})^{z-m}]}{(\frac{i}{12})}\\ \textup{Principal}(z)&=0. \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-c7dfcd4a9292b2acc5f43cd3ffadc640_l3.png)
Adding the ![]() interest and capital component gives us the
interest and capital component gives us the ![]() repayment amount:
repayment amount:
![]()
This is the last repayment amount which is smaller or equal to ![]() that closes off the loan.
that closes off the loan.
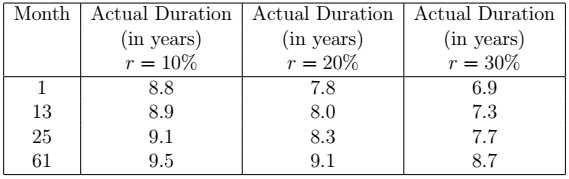
Consider a 10-year 8% loan. The next table gives the actual duration of the loan given an increase of ![]() in the repayments, starting from month
in the repayments, starting from month ![]() . For simplicity,we consider only five case: the case when the increase in repayments starts from the first the repayment, after 1 year of repayments, after 2 years of repayments and after 5 years of repayments.
. For simplicity,we consider only five case: the case when the increase in repayments starts from the first the repayment, after 1 year of repayments, after 2 years of repayments and after 5 years of repayments.
 and
and  values
valuesThe next three figures show the prepayment curves for the 10-year 8% loan when ![]() =10%, 20% and 30% respectively, with various values of
=10%, 20% and 30% respectively, with various values of ![]() .
.

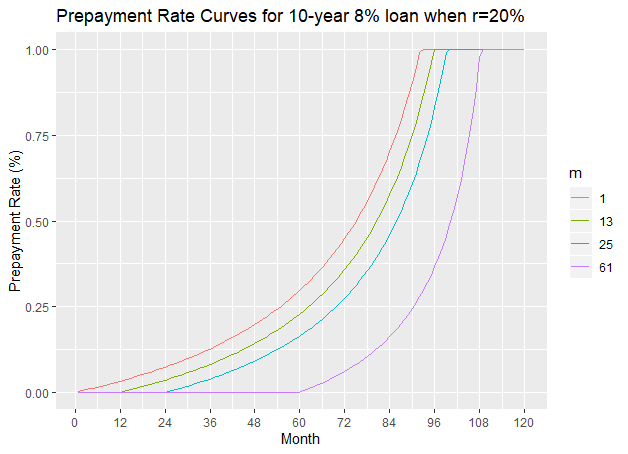

Consider a 20-year ![]() loan. The next table gives the actual duration of the loan given an increase of
loan. The next table gives the actual duration of the loan given an increase of ![]() in the repayments, starting from month
in the repayments, starting from month ![]() . For simplicity, we consider only five case: the case when the increase in repayments starts from the first the repayment, after 1 year of repayments, after 2 years of repayments, after 5 years of repayments, after 10 years of repayments, and after 15 years of repayments.
. For simplicity, we consider only five case: the case when the increase in repayments starts from the first the repayment, after 1 year of repayments, after 2 years of repayments, after 5 years of repayments, after 10 years of repayments, and after 15 years of repayments.

 and
and 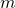 values
valuesThe next three figures show the prepayment curves for the 20-year 3% loan when ![]() =10%, 20% and 30% respectively.
=10%, 20% and 30% respectively.
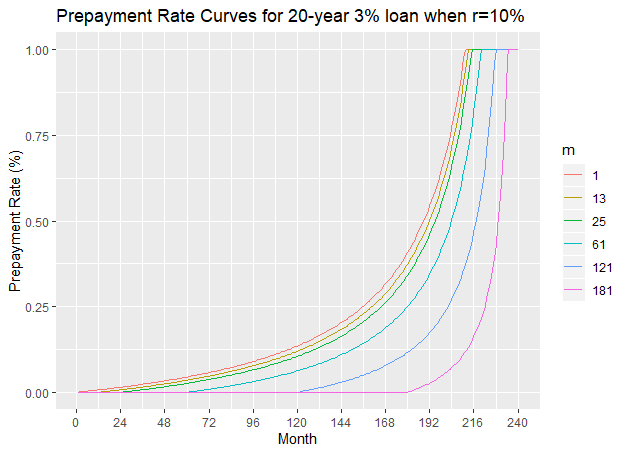
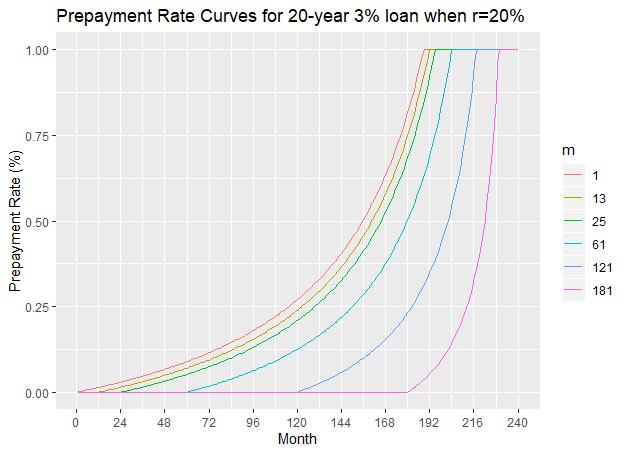
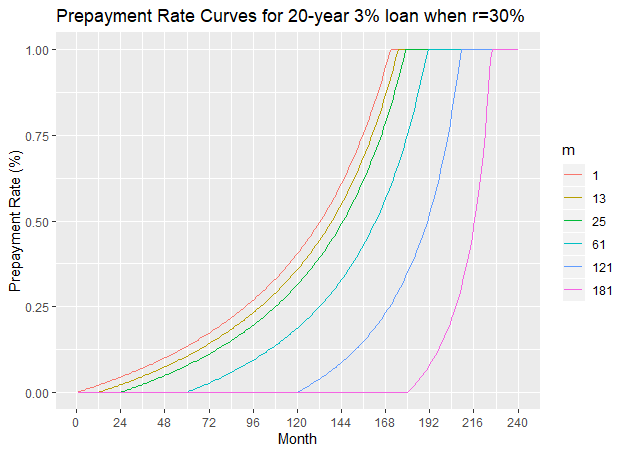
We can also calculate the loss of interest income, when the prepayment starts at month ![]() .
.
Result 7: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the amount repaid monthly till month
be the amount repaid monthly till month ![]() and let
and let ![]() be the actual repayment amount from month
be the actual repayment amount from month ![]() onwards, where the value
onwards, where the value ![]() as calculated in Equation (1). The loss of interest in the
as calculated in Equation (1). The loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss}(k)=\begin{cases} 0, & \textup{for }k<m\\rR[(1+\frac{i}{12})^{k-m}-1], & \textup{for }m\leq k \leq z\\R[1-(1+\frac{i}{12})^{k-n-1}], & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-13cc150a19b8943b651a5af2227bc06e_l3.png)
Proof: Similar to that of Result 3. ![]()
Alternatively, the Interest Loss at month ![]() could be represented by:
could be represented by:
![]()
The Interest Loss Percentage at the ![]() month is given by the following result.
month is given by the following result.
Result 8: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the amount repaid monthly till month
be the amount repaid monthly till month ![]() and let
and let ![]() be the actual repayment amount from month
be the actual repayment amount from month ![]() onwards, where the value
onwards, where the value ![]() as calculated in Equation (1). The percentage of loss of interest in the
as calculated in Equation (1). The percentage of loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss Percentage}(k)=\begin{cases} 0\%, & \textup{for }k<m\\\frac{r[(1+\frac{i}{12})^{k-m}-1]}{1-(1+\frac{i}{12})^{k-n-1}}\times 100\%, & \textup{for }m\leq k \leq z\\100\%, & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-8b8e2d8d1e27ffb25a7934d5a8c3d851_l3.png)
Hence Results 3 and 4 can be viewed as special cases of Results 7 and 8 when ![]() .
.
Let us consider the total interest paid on the loan in the case of having prepayments starting from the ![]() month.
month.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \textup{Total Interest Paid}&=\sum_{k=1}^{z} \textup{Interest Component}(k)\\ &=\frac{P}{1-(1+\frac{i}{12})^{-n}}[(1+\frac{i}{12})^{-n}-(1+\frac{i}{12})^{z-n}+(1+r)z(\frac{i}{12})-rm(\frac{i}{12})+r(1+\frac{i}{12})-r(1+\frac{i}{12})^{z-m+1}]. \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-99c7900c3cd7a9b5db924be3f18550fc_l3.png)
The fraction of the Total Interest Paid over the Principal amount is thus given by:
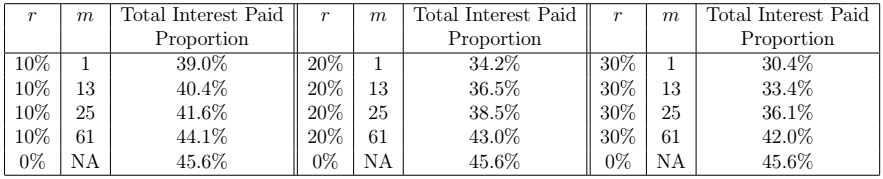
The next two tables gives the Total Interest Paid Proportion for the 10-year 8% loan and the 20-year 3% loan, for different values of ![]() and
and ![]() . Note that
. Note that ![]() =0% is the case when there is no prepayment present. Note that the higher the
=0% is the case when there is no prepayment present. Note that the higher the ![]() value and the earlier the repayments starts, the lower the Total Interest Rate Proportion.
value and the earlier the repayments starts, the lower the Total Interest Rate Proportion.
 and
and 
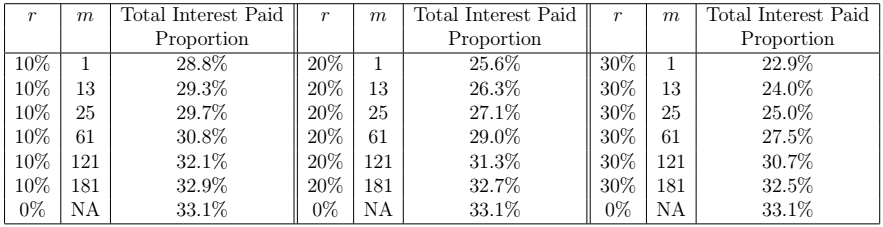
 and
and 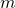
Now we calculate the Total Interest Loss which is given by the following equation.
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \textup{Total Interest Loss}&=\sum_{k=1}^{n}\textup{Interest Loss}(k)=\textup{Total Interest Paid}_{RS}-\textup{Total Interest Paid}_{Prep.}\\ &=\frac{P}{1-(1+\frac{i}{12})^{-n}}[\frac{i}{12}n-1+(1+\frac{i}{12})^{z-n}-(1+r)z(\frac{i}{12})+rm(\frac{i}{12})-r(1+\frac{i}{12})+r(1+\frac{i}{12})^{z-m+1}]. \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-b55c90996b5673912dd2cccdcbd12af7_l3.png)
The Total Interest Loss Proportion is thus given by:
![]()
The next tables give the Total Interest Loss Proportion for the 10-year 8% loan and the 20-year 3% loan, for different values of ![]() and
and ![]() .
.

 and
and 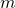
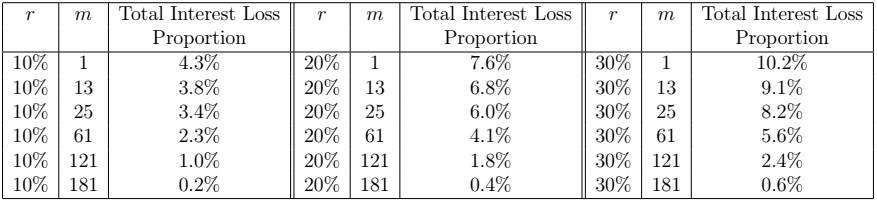
 and
and 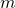
Prepayment on a Portfolio of Loans
Suppose that we have a portfolio of ![]() loans. A loan is initiated at time
loans. A loan is initiated at time ![]() (that is the drawdown is at
(that is the drawdown is at ![]() and the first repayment starts at
and the first repayment starts at ![]() ), has principal
), has principal ![]() , yearly interest rate
, yearly interest rate ![]() , and duration
, and duration ![]() , for
, for ![]() . Suppose that the time is a non-negative integer, set
. Suppose that the time is a non-negative integer, set ![]() and let the time now be
and let the time now be ![]() . Suppose that each repayment of each loan from time
. Suppose that each repayment of each loan from time ![]() onwards is increased by a factor of
onwards is increased by a factor of ![]() . We would like to know the outstanding principal of the whole portfolio at each time
. We would like to know the outstanding principal of the whole portfolio at each time ![]() from
from ![]() onwards, given that prepayment is present and compare it to that when prepayment is not present.
onwards, given that prepayment is present and compare it to that when prepayment is not present.
The outstanding principal of the whole portfolio ![]() at time
at time ![]() for
for ![]() , in the case where prepayment is not present is given by:
, in the case where prepayment is not present is given by:
(3) 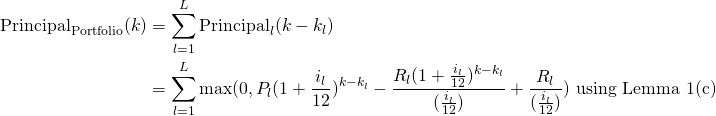
where ![]() is the outstanding principal of the
is the outstanding principal of the ![]() loan at time
loan at time ![]() .
.
Similarly, the outstanding principal of the whole portfolio ![]() for
for ![]() in the case when the prepayments start at
in the case when the prepayments start at ![]() is given by:
is given by:
(4) ![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Principal}_{\textup{Portfolio}}^{\textup{Prep.}}(k)=&\sum_{l=1}^{L} \textup{Principal}_l^{\textup{Prep.}}(k-k_l)\\=&\sum_{l=1}^{L} \max(0,P_l(1+\frac{i_l}{12})^{k-k_l}-\frac{R_l(1+\frac{i_l}{12})^{k-k_l}}{(\frac{i_l}{12})}+\frac{R_l}{(\frac{i_l}{12})})+\frac{rR_l[1-(1+\frac{i_l}{12})^{k-\kappa}]}{(\frac{i_l}{12})}) \textup{ using Lemma 4(c)}\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-d9e5e859a7e20b9173dcc0862689d12f_l3.png)
where ![]() is the outstanding principal of the
is the outstanding principal of the ![]() loan at time
loan at time ![]() .
.
We define the prepayment of the portfolio ![]() at time
at time ![]() as the sum of the extra capital repaid of each loan, at time
as the sum of the extra capital repaid of each loan, at time ![]() . Thus for
. Thus for ![]() we have the equation:
we have the equation:
(5) ![]()
We define the prepayment rate of the portfolio of loans ![]() at time
at time ![]() as the sum of extra capital repaid of each loan divided by the total outstanding principal of the loans given that prepayment is not present:
as the sum of extra capital repaid of each loan divided by the total outstanding principal of the loans given that prepayment is not present:
(6) ![]()
The expected inflow of interest income at month ![]() is sum of the interest components at month
is sum of the interest components at month ![]() of all the loans of the portfolio, given that prepayment is not present. This is given by the equation:
of all the loans of the portfolio, given that prepayment is not present. This is given by the equation:
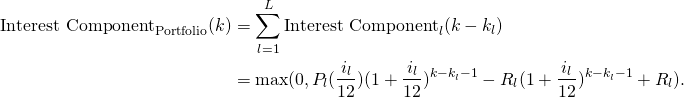
The actual inflow of interest income at month ![]() is sum of the interest components at month
is sum of the interest components at month ![]() of all the loans of the portfolio, given that prepayment is present. This is given by the equation:
of all the loans of the portfolio, given that prepayment is present. This is given by the equation:
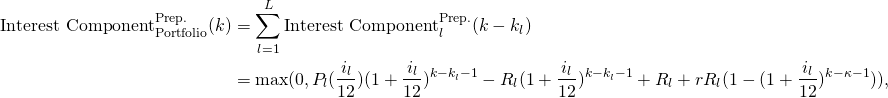
for ![]() , where
, where ![]() is the interest component in the
is the interest component in the ![]() month of loan
month of loan ![]() , given that prepayment starts from month
, given that prepayment starts from month ![]() .
.
The Interest Loss on the whole portfolio at time ![]() , for
, for ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \textup{Interest Loss}_\textup{Portfolio}(k)&=\sum_{l=1}^{L} \textup{Interest Loss}_l(k-k_l)\times\chi_{\lbrace k -k_l\leq n_l\rbrace}\\ &=\sum_{l=1}^{L} \max(0,\min(rR_l[(1+\frac{i_l}{12})^{k-\kappa-1}-1],R_l[1-(1+\frac{i_l}{12})^{k-k_l-n_l-1}]))\times\chi_{\lbrace k -k_l\leq n_l\rbrace} \end{split} \end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-f6b608944016d0ef9ded35de9a6088cb_l3.png)
where ![]() is the interest loss on loan
is the interest loss on loan ![]() at month
at month ![]() and
and ![]() if
if ![]() or 0 otherwise.
or 0 otherwise.
Consider the following example. Suppose we have a portfolio made up of three loans as characterised in the next table.

Let the time now be ![]() and suppose that each repayment from time
and suppose that each repayment from time ![]() onwards increases by a factor of
onwards increases by a factor of ![]() and we take
and we take ![]() to be equal to
to be equal to ![]() as an example. The next table gives some results derived from Equations (3), (4), (5) and (6) respectively. Note that the month numbers are chosen at an interval of 12. So the row corresponding to 84 shows the state of the portfolio after a year of prepayments, the row corresponding to 96 shows the state of the portfolio after two years of prepayments and so on.
as an example. The next table gives some results derived from Equations (3), (4), (5) and (6) respectively. Note that the month numbers are chosen at an interval of 12. So the row corresponding to 84 shows the state of the portfolio after a year of prepayments, the row corresponding to 96 shows the state of the portfolio after two years of prepayments and so on.

 =10%
=10%The next figure shows the portfolio prepayment rate curves for r=10%, 20% and 30%.
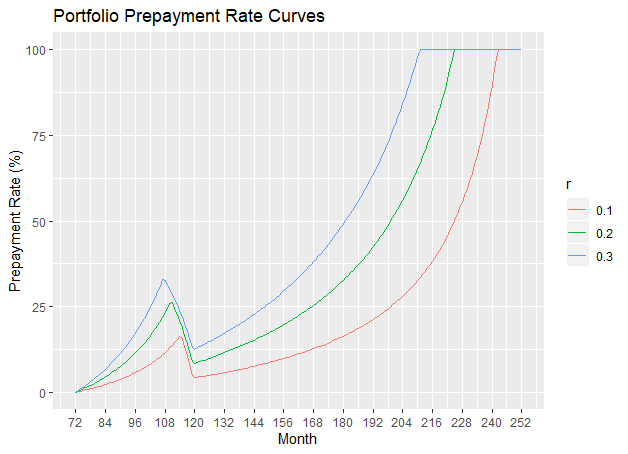
 =10%, 20% and 30%
=10%, 20% and 30%Consider the prepayment rate curve for ![]() =10%. This reaches a local maximum of 16.3% at month 114, which is the month before both Loan 1 and Loan 3 are repaid in full. It reaches a local minimum at month 120, by which time the outstanding principal of both Loan 1 and Loan 3 have reached an outstanding principal of 0 according to their respective repayment schedules (excluding prepayment). From that month onwards, the prepayment rate curve keeps on increasing to reach 100% at which time Loan 3 is repaid in full. Note that since the repayment schedule (excluding prepayment) is independent of
=10%. This reaches a local maximum of 16.3% at month 114, which is the month before both Loan 1 and Loan 3 are repaid in full. It reaches a local minimum at month 120, by which time the outstanding principal of both Loan 1 and Loan 3 have reached an outstanding principal of 0 according to their respective repayment schedules (excluding prepayment). From that month onwards, the prepayment rate curve keeps on increasing to reach 100% at which time Loan 3 is repaid in full. Note that since the repayment schedule (excluding prepayment) is independent of ![]() , all the three prepayment rate curves reach a local minimum at month 120.
, all the three prepayment rate curves reach a local minimum at month 120.
One could then derive the next table which shows the inflow of portfolio principal during the next five years. The expected principal inflow is the sum of the capital portion of each repayment during a particular year, while the actual principal inflow is the sum of the capital portion of each repayment during a particular year given that prepayment is present.
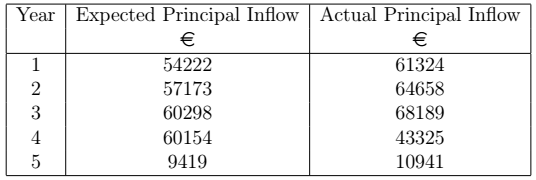
 =10%
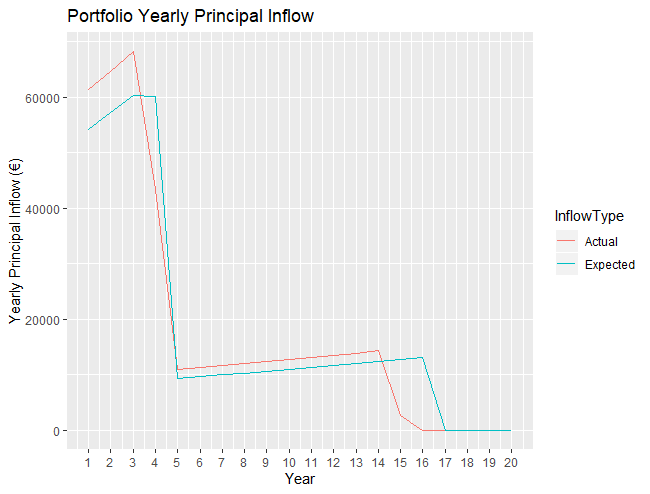
=10%The next figure offers a visualisation of an extension of the data given in the previous table. It shows a plot of the expected and actual inflow of principal (for ![]() =10%) over the next 20 years.
=10%) over the next 20 years.
 =10%
=10%Next we consider the expected and actual inflow of interest income. The next graph shows the monthly inflow of expected interest income and the actual interest income given the increase in the repayments of r=10%, 20% and 30%.
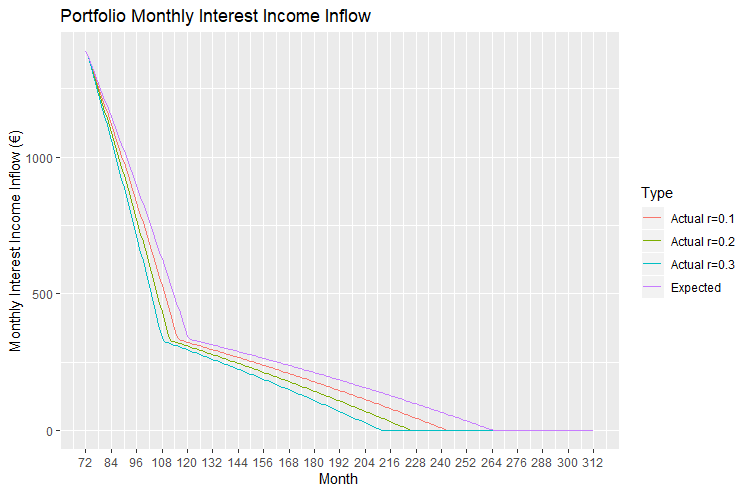
These monthly figures can be group in order to obtain the yearly expected and actual inflow of interest income. The next table gives the annual inflow of interest income, both expected and actual, during the next five years for ![]() =10%. Their difference results in the loss of interest income over a yearly basis. The loss can be expressed a percentage by computing the fraction of yearly interest loss over the expected yearly inflow of interest income.
=10%. Their difference results in the loss of interest income over a yearly basis. The loss can be expressed a percentage by computing the fraction of yearly interest loss over the expected yearly inflow of interest income.
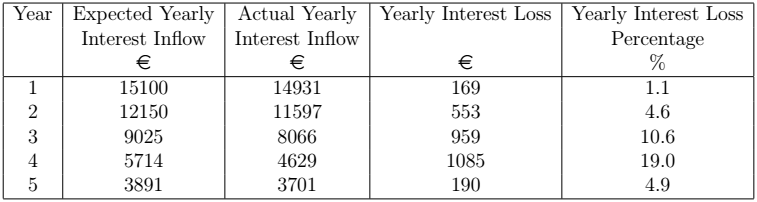
 =10%
=10%Prepayment from a decrease in the interest rate
In what follows, we consider the prepayment in the loan resulting from a decrease in the interest rate whilst the monthly repayment is kept constant, and not revised according the new interest rate. We consider a loan with principal ![]() , interest rate
, interest rate ![]() and term
and term ![]() months. Each monthly repayment will always be equal to
months. Each monthly repayment will always be equal to ![]() as given by Equation (1) (even when prepayment is present). The interest rate
as given by Equation (1) (even when prepayment is present). The interest rate ![]() will decrease to a lower new interest rate
will decrease to a lower new interest rate ![]() . In the next section, we will consider the case when the change in interest rate happens exactly at the time of draw-down (at month 0). This will be generalised to the case when the change in the interest rate happens at any month
. In the next section, we will consider the case when the change in interest rate happens exactly at the time of draw-down (at month 0). This will be generalised to the case when the change in the interest rate happens at any month ![]() .
.
Constant Prepayment from Month 1 resulting from a decrease in the interest rate
Let us assume that the interest rate changes from ![]() to
to ![]() exactly at the time of draw-down. Hence the borrower starts making prepayments from the first repayment (at month 1). We are after: (1) the prepayment rate at each month (2) the actual duration of the loan. First, from Lemma 5 we can deduce the capital component, the interest component and outstanding principal in this case.
exactly at the time of draw-down. Hence the borrower starts making prepayments from the first repayment (at month 1). We are after: (1) the prepayment rate at each month (2) the actual duration of the loan. First, from Lemma 5 we can deduce the capital component, the interest component and outstanding principal in this case.
Lemma 5: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let the interest rate be decreased to a new yearly interest rate
months. Let the interest rate be decreased to a new yearly interest rate ![]() . Let
. Let ![]() be the monthly repayment as calculated in Equation (1) and let
be the monthly repayment as calculated in Equation (1) and let ![]() be the actual duration of the loan, given that prepayment is present. The interest and capital component in the
be the actual duration of the loan, given that prepayment is present. The interest and capital component in the ![]() repayment and the outstanding principal at month
repayment and the outstanding principal at month ![]() , for
, for ![]() are given by:
are given by:

Proof: By induction on ![]() .
. ![]()
Result 9: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let the interest rate be decreased to
months. Let the interest rate be decreased to ![]() at month 0. Then the prepayment rate at month
at month 0. Then the prepayment rate at month ![]() , for
, for ![]() is:
is:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Prepayment Rate}(k)=\frac{1-\frac{i}{i'}-(1+\frac{i}{12})^{k-n}+(1+\frac{i'}{12})^k[(1+\frac{i}{12})^{-n}+\frac{i}{i'}-1]}{1-(1+\frac{i}{12})^{k-n}}.\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-80f0e5a6d28356bbb9bd78e195361325_l3.png)
Proof:
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\text{Prepayment Rate}(k)&= \frac{\text{Principal}_{\text{RS}}(k)-\text{Principal}_{\text{Actual}}(k)}{\text{Principal}_{\text{RS}}(k)} \text{ (by Equation (2)})\\&=\frac{P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}-P(1+\frac{i'}{12})^k+\frac{R(1+\frac{i'}{12})^k}{(\frac{i'}{12})}-\frac{R}{(\frac{i'}{12})}}{P(1+\frac{i}{12})^k-\frac{R(1+\frac{i}{12})^k}{(\frac{i}{12})}+\frac{R}{(\frac{i}{12})}}\text{ (by Lemma 1(c) and Lemma 5(c))}\\&=\frac{1-\frac{i}{i'}-(1+\frac{i}{12})^{k-n}+(1+\frac{i'}{12})^k[(1+\frac{i}{12})^{-n}+\frac{i}{i'}-1]}{1-(1+\frac{i}{12})^{k-n}}. $\square$\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-6ae3f775795a0be896143f471445cb11_l3.png)
Result 10: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. When the interest rate is decreased to
months. When the interest rate is decreased to ![]() at month 0, the actual duration of the loan is:
at month 0, the actual duration of the loan is:
![]()
Proof: Let ![]() be the least integer such that the prepayment rate is greater or equal to 1. Then
be the least integer such that the prepayment rate is greater or equal to 1. Then ![]() is the actual duration of the loan. Note that we assume that
is the actual duration of the loan. Note that we assume that ![]() and hence
and hence ![]() .
.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\text{Prepayment Rate}(k)&\geq 1\\\frac{1-\frac{i}{i'}-(1+\frac{i}{12})^{k-n}+(1+\frac{i'}{12})^k[(1+\frac{i}{12})^{-n}+\frac{i}{i'}-1]}{1-(1+\frac{i}{12})^{k-n}}&\geq 1\text{ (by Result 9)}\\(1+\frac{i'}{12})^k[(1+\frac{i}{12})^{-n}+\frac{i}{i'}-1]-\frac{i}{i'} & \geq 0\\(1+\frac{i'}{12})^k &\geq \frac{\frac{i}{i'}}{\frac{i}{i'}-1+(1+\frac{i}{12})^{-n}}\\k&\geq \frac{\ln{\frac{i}{i'}}-\ln{[\frac{i}{i'}-1+(1+\frac{i}{12})^{-n}]}}{\ln{(1+\frac{i'}{12})}}.\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-37f25e5b159e7b79bfe2561b2f3ebd81_l3.png)
Hence result follows.
Note that Results 9 and 10 are independent of the principal ![]() . Note also that in the trivial case when
. Note also that in the trivial case when ![]() , the actual duration is equal to the initial duration
, the actual duration is equal to the initial duration ![]() . At month
. At month ![]() , the loan is paid in full, and hence the prepayment rate at month
, the loan is paid in full, and hence the prepayment rate at month ![]() is equal to 1. In fact, at month
is equal to 1. In fact, at month ![]() , we have:
, we have:
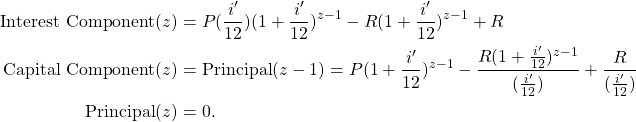
Adding the ![]() interest and capital component gives us the
interest and capital component gives us the ![]() repayment amount:
repayment amount:
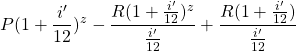
This is the last repayment amount which is smaller or equal to ![]() that closes off the loan.
that closes off the loan.
Let us consider some examples of loans and different scenarios of ![]() , for which we calculate the actual duration of the loan and plot prepayment rate curves.
, for which we calculate the actual duration of the loan and plot prepayment rate curves.
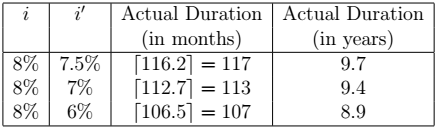
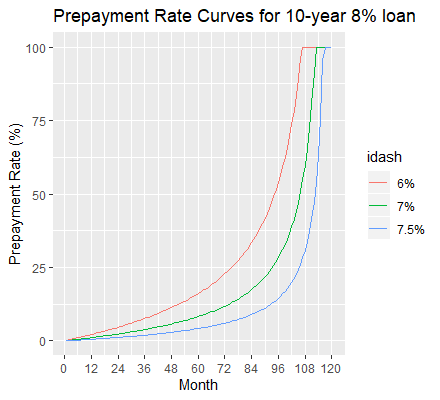
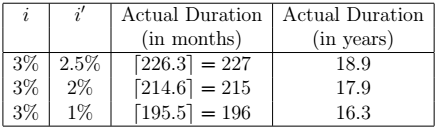
Consider a loan with an initial interest rate ![]() and an initial duration of 10 years (
and an initial duration of 10 years (![]() ). Let the interest rate be changed to
). Let the interest rate be changed to ![]() where
where ![]() ,
, ![]() and
and ![]() . The next table gives the actual duration (using Result 10) of the loan given these particular values of
. The next table gives the actual duration (using Result 10) of the loan given these particular values of ![]() .
.
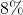 interest rate for various
interest rate for various 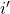 values
valuesThe next figure shows the prepayment curves for the 10-year 8% loan when ![]() takes on values 7.5%, 7% and 6%.
takes on values 7.5%, 7% and 6%.
Consider a loan with an interest rate of ![]() and an initial duration of 20 years (
and an initial duration of 20 years (![]() ). We consider three values of
). We consider three values of ![]() :
: ![]() ,
, ![]() and
and ![]() . The next table gives the actual duration of this loan for the different values of
. The next table gives the actual duration of this loan for the different values of ![]() and the next figure shows the corresponding prepayment curves.
and the next figure shows the corresponding prepayment curves.
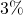 interest rate for various
interest rate for various 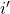 values
values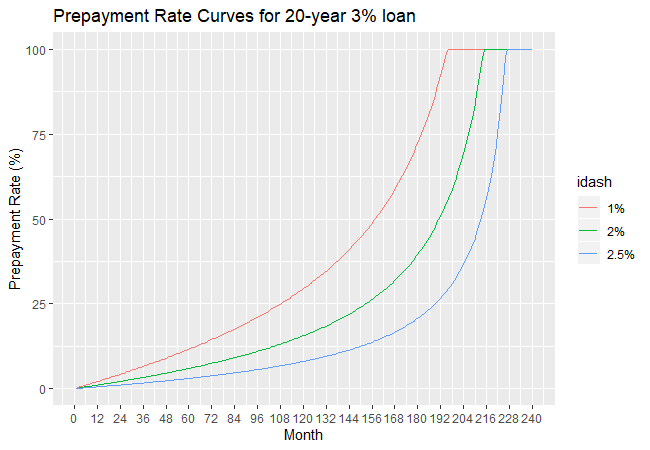
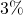 loan for various values of
loan for various values of 
We calculate the interest income lost at each month resulting from the prepayments induced by the decrease in interest rate.
Result 11: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the repayment amount as calculated in Equation (1) and let the interest rate be decreased to
be the repayment amount as calculated in Equation (1) and let the interest rate be decreased to ![]() at month 0. The loss of interest in the
at month 0. The loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss}(k)=\begin{cases}R[(1+\frac{i'}{12})^{k-1}(1+\frac{i'}{i}(1+i/12)^{-n}-\frac{i'}{i})-(1+\frac{i}{12})^{k-n-1}], & \textup{for }1\leq k \leq z\\R[1-(1+\frac{i}{12})^{k-n-1}], & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-7b5bfd510dd1d838e78fcc787df6645d_l3.png)
Proof: Similar to that of Result 3. ![]()
We can consider the fraction of the interest loss from the expected amount of interest receivable. We calculate Interest Loss Percentage, which is the fraction of the interest loss from the expected amount of interest receivable.
Result 12: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the repayment amount as calculated in Equation (1) and let the interest rate be decreased to
be the repayment amount as calculated in Equation (1) and let the interest rate be decreased to ![]() at month 0. The percentage of loss of interest in the
at month 0. The percentage of loss of interest in the ![]() month is given by:
month is given by:
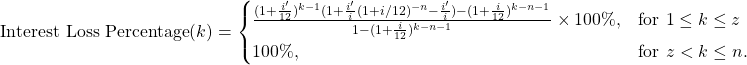
The next two figures show the plot of Interest Loss Percentage for two loans: a 10-year ![]() loan and a 20-year
loan and a 20-year ![]() loan. The curves all start at a value of
loan. The curves all start at a value of ![]() at month 1. Then they increase to 100
at month 1. Then they increase to 100![]() at time
at time ![]() when the loan is repaid in full prematurely.
when the loan is repaid in full prematurely.

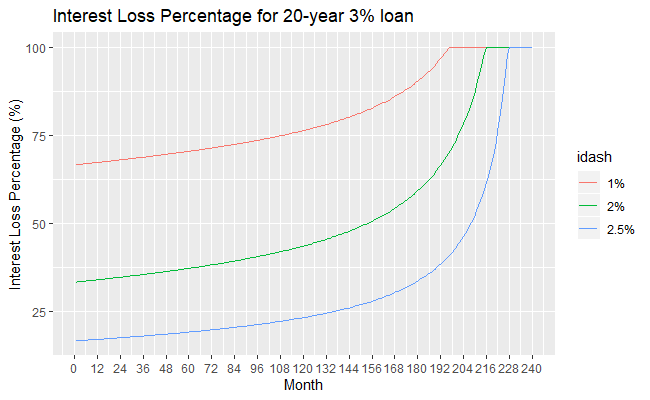
Interest Loss Percentage in the repayments of a 10-year ![]() loan and a 20-year
loan and a 20-year ![]() loan respectively
loan respectively
Let us consider the total interest paid on the loan in the case of having prepayments starting from the first month.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Total Interest Paid}&=\sum_{k=1}^{z} \textup{Interest Component}(k)\\&=\frac{P[((1+\frac{i'}{12})^z-1)(1-(1+\frac{i}{12})^{-n})+\frac{i}{i'}(1-(1+\frac{i'}{12})^z)+\frac{i}{12}z]}{1-(1+\frac{i}{12})^{-n}}.\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-58be5f4ba002f1000d71dfdde08017f4_l3.png)
The fraction of the Total Interest Paid over the Principal amount is thus given by:
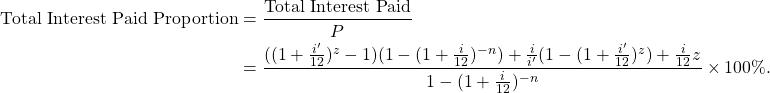
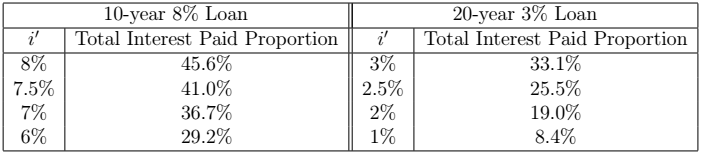
The next table gives the Total Interest Paid Proportion for the 10-year ![]() loan and the 20-year
loan and the 20-year ![]() loan, for different values of
loan, for different values of ![]() . For comparison we show the total interest paid proportion for the case when
. For comparison we show the total interest paid proportion for the case when ![]() , that is, when no prepayment present.
, that is, when no prepayment present.
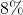 Loan and 20-year
Loan and 20-year 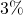 Loan
LoanThe Total Interest Loss which is the total interest which is lost on a loan due to prepayments is given by the following formula.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Total Interest Loss}&=\sum_{k=1}^{n}\textup{Interest Loss}(k)=\textup{Total Interest Paid}_{RS}-\textup{Total Interest Paid}_{Prep.}\\&=\frac{P[\frac{i}{12}(n-z)+(1+\frac{i'}{12})^{z}((1+\frac{i}{12})^{-n}+\frac{i'}{i}-1)-\frac{i}{i'}]}{1-(1+\frac{i}{12})^{-n}}.\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-02fe17059310ee7fd6138f2f6268d5ac_l3.png)
The Total Interest Loss Proportion is thus given by:

The next table gives the Total Interest Loss Proportion for the 10-year ![]() loan and the 20-year
loan and the 20-year ![]() loan, for different values of
loan, for different values of ![]() .
.

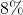 Loan and 20-year
Loan and 20-year 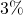 Loan
LoanConstant Prepayment from Month 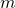 resulting from a decrease in the interest rate
resulting from a decrease in the interest rate
Suppose now that the decrease in the interest rate happens exactly at the time of the ![]() repayment, that is, at month
repayment, that is, at month ![]() . Hence the prepayments start from month
. Hence the prepayments start from month ![]() . The interest and capital components from the
. The interest and capital components from the ![]() month repayment onwards change as follows.
month repayment onwards change as follows.
Lemma 6: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to
be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to ![]() at month
at month ![]() . Let
. Let ![]() be the actual duration of the loan, given that prepayment is present. The interest and capital component in the
be the actual duration of the loan, given that prepayment is present. The interest and capital component in the ![]() repayment and the outstanding principal at month
repayment and the outstanding principal at month ![]() , for
, for ![]() are given by:
are given by:
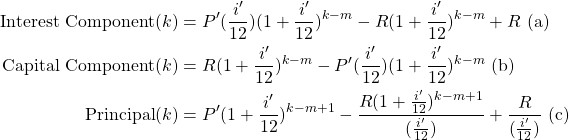
where
Proof: By induction on ![]() .
. ![]()
Result 13 gives the prepayment rate at each month.
Result 13: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. Let
months. Let ![]() be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to
be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to ![]() at month
at month ![]() . Let
. Let ![]() be the actual duration of the loan, given that prepayment is present. The prepayment rate at month
be the actual duration of the loan, given that prepayment is present. The prepayment rate at month ![]() for
for ![]() is 0, whilst the prepayment rate at month
is 0, whilst the prepayment rate at month ![]() for
for ![]() is:
is:
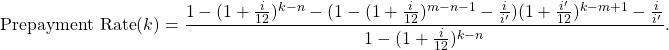
Proof: The proof is similar to that of Result 1. ![]()
Note that Result 9 can now be viewed as a corollary of Result 13 obtained by fixing ![]() to be 1. Result 14 gives a formula for the actual duration
to be 1. Result 14 gives a formula for the actual duration ![]() .
.
Result 14: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and duration
compounded monthly and duration ![]() months. When the interest rate is decreased to
months. When the interest rate is decreased to ![]() at month
at month ![]() , the actual duration of the loan is:
, the actual duration of the loan is:
![]()
\end{result}
Proof: The proof is similar to that of Result 2. ![]()
Result 10 can now be seen as a corollary of Result 14 for the case when ![]() .
.
At month ![]() , the loan is paid in full, and hence the prepayment rate at month
, the loan is paid in full, and hence the prepayment rate at month ![]() is equal to 1. In fact, at month
is equal to 1. In fact, at month ![]() , we have:
, we have:
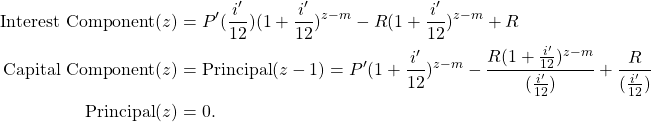
Adding the ![]() interest and capital component gives us the
interest and capital component gives us the ![]() repayment amount:
repayment amount:
![]()
This is the last repayment amount which is smaller or equal to ![]() that closes off the loan.
that closes off the loan.
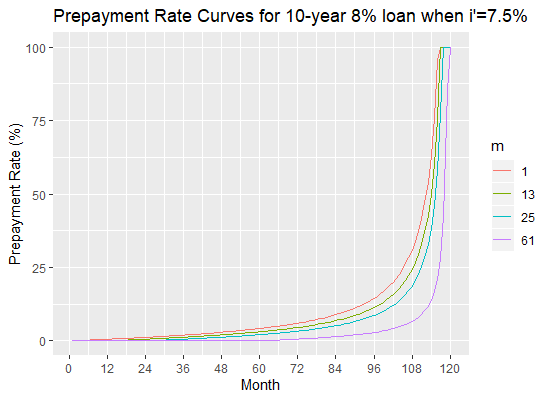
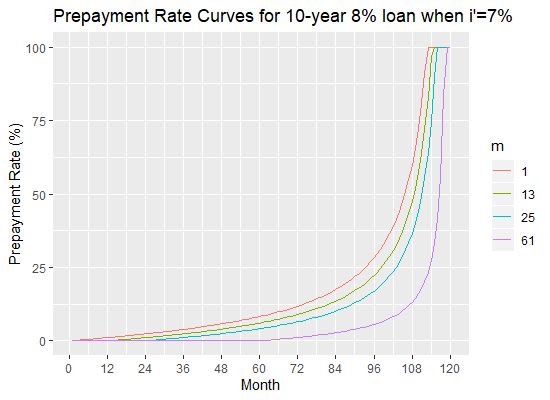
Consider a 10-year ![]() loan. The next table gives the actual duration of the loan given a change of interest rate to
loan. The next table gives the actual duration of the loan given a change of interest rate to ![]() at month
at month ![]() . For simplicity, we consider only five case: the case when the prepayments start from the first the repayment, after 1 year of repayments, after 2 years of repayments and after 5 years of repayments.
. For simplicity, we consider only five case: the case when the prepayments start from the first the repayment, after 1 year of repayments, after 2 years of repayments and after 5 years of repayments.
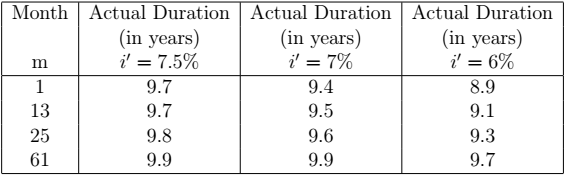
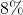 interest rate for various
interest rate for various 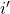 and
and 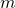 values
valuesThe next three figures show the prepayment curves for the 10-year 8\% loan when i’=7.5\%, 7\% and 6\% respectively, with various values of ![]() .
.
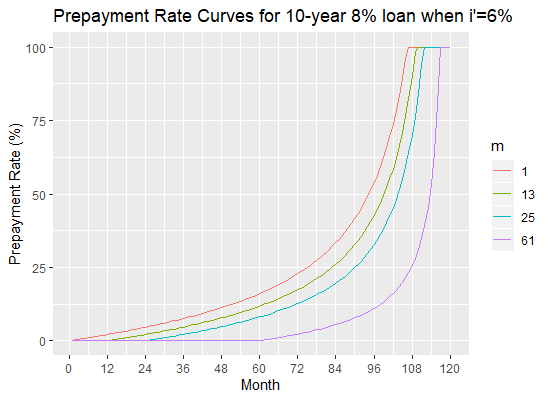
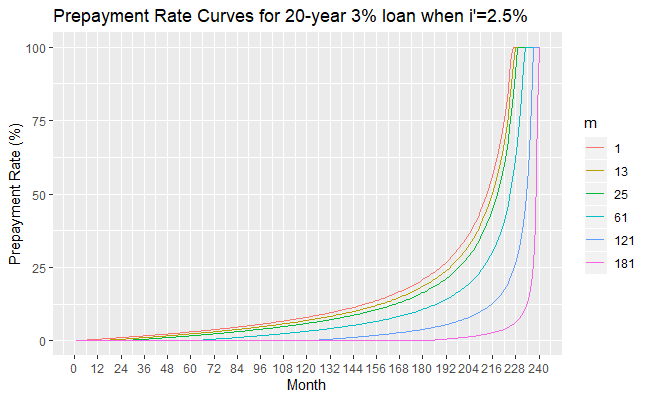
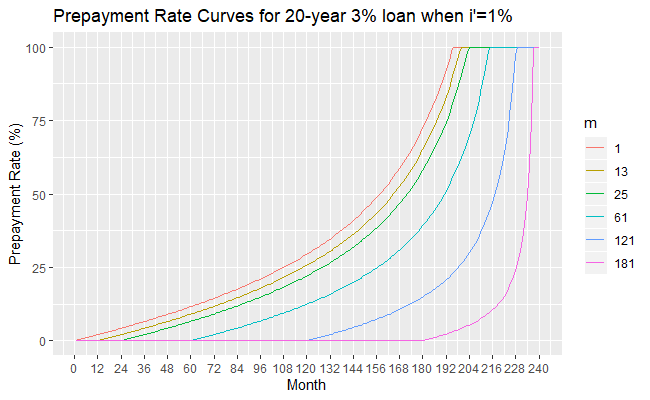
Consider a 20-year ![]() loan. The next table gives the actual duration of the loan given a decrease in the interest rate decrease to
loan. The next table gives the actual duration of the loan given a decrease in the interest rate decrease to ![]() in month
in month ![]() . For simplicity, we consider only five case: the case when the prepayment starts from the first the repayment, after 1 year of repayments, after 2 years of repayments, after 5 years of repayments, after 10 years of repayments, and after 15 years of repayments.
. For simplicity, we consider only five case: the case when the prepayment starts from the first the repayment, after 1 year of repayments, after 2 years of repayments, after 5 years of repayments, after 10 years of repayments, and after 15 years of repayments.
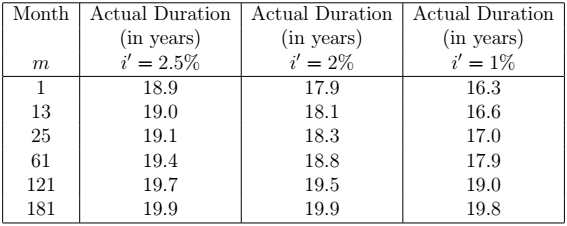
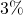 interest rate for various
interest rate for various 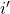 and
and 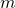 values
valuesThe next three figures show the prepayment curves for the 20-year 3\% loan when ![]() and
and ![]() respectively.
respectively.

We can also calculate the loss of interest income, when the prepayment starts at month ![]() .
.
Result 15: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to
be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to ![]() at month
at month ![]() . The loss of interest in the
. The loss of interest in the ![]() month is given by:
month is given by:
![Rendered by QuickLaTeX.com \begin{equation*}\textup{Interest Loss}(k)=\begin{cases} 0, & \textup{for }k<m\\R[(1+\frac{i'}{12})^{k-m}(1-\frac{i'}{i}+(\frac{i'}{i})(1+\frac{i}{12})^{m-n-1})-(1+\frac{i}{12})^{k-n-1}], & \textup{for }m\leq k \leq z\\R[1-(1+\frac{i}{12})^{k-n-1}], & \textup{for }z< k \leq n.\end{cases}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-e7daeef55881ad54505b72a815d0607c_l3.png)
Proof: Similar to that of Result 3. ![]()
The Interest Loss Percentage at the ![]() month is given by the following result.
month is given by the following result.
Result 16: Consider a loan with associated principal ![]() , yearly interest rate
, yearly interest rate ![]() compounded monthly and initial duration
compounded monthly and initial duration ![]() months. Let
months. Let ![]() be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to
be the amount repaid monthly as calculated in Equation (1) and let the interest rate be decreased to ![]() at month
at month ![]() . The percentage of loss of interest in the
. The percentage of loss of interest in the ![]() month is given by:
month is given by:
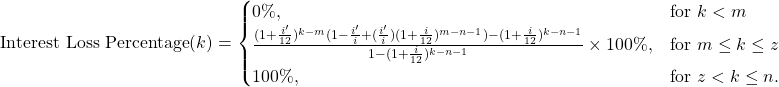
\end{result}
Hence Results 11 and 12 can be viewed as special cases of Results 15 and 16 when ![]() .
.
Let us consider the total interest paid on the loan in the case of having prepayments starting from the ![]() month.
month.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Total Interest Paid}&=\sum_{k=1}^{z} \textup{Interest Component}(k)\\&=\frac{P}{1-(1+\frac{i}{12})^{-n}}[z(\frac{i}{12})+(1+\frac{i}{12})^{-n}-1+\frac{i}{i'}+(1-(1+\frac{i}{12})^{m-n-1}-\frac{i}{i'})(1+\frac{i'}{12})^{z-m+1}].\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-2bf4c44c568db216be54b8814b7f2136_l3.png)
The fraction of the Total Interest Paid over the Principal amount is thus given by:
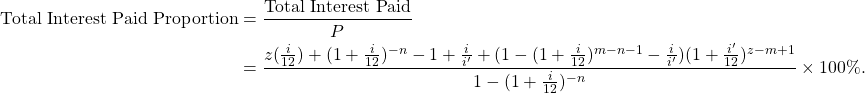
The next two tables give the Total Interest Paid Proportion for the 10-year 8\% loan and the 20-year 3\% loan respectively, for different values of ![]() and
and ![]() . Note that
. Note that ![]() is the case when there is no prepayment present. Note that the lower the
is the case when there is no prepayment present. Note that the lower the ![]() value and the earlier the repayments starts, the lower the Total Interest Rate Proportion.
value and the earlier the repayments starts, the lower the Total Interest Rate Proportion.
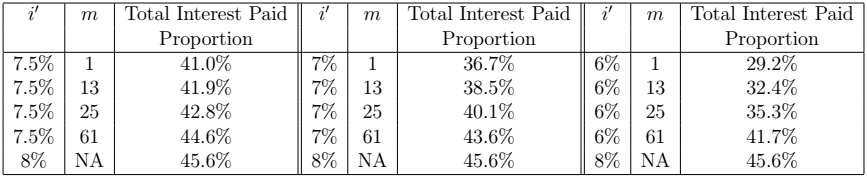
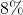 Loan for various
Loan for various 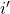 and
and 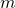 values
values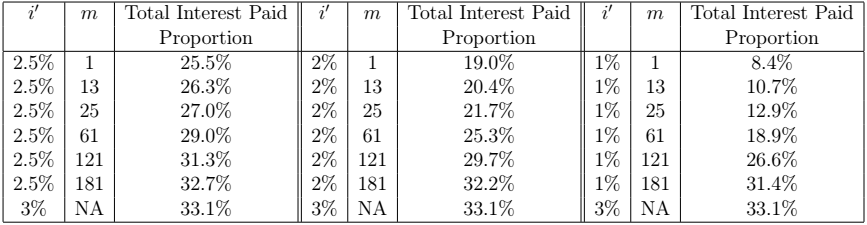
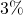 Loan for various
Loan for various 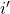 and
and 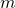 values
valuesNow we calculate the Total Interest Loss which is given by the following equation.
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\textup{Total Interest Loss}&=\sum_{k=1}^{n}\textup{Interest Loss}(k)=\textup{Total Interest Paid}_{RS}-\textup{Total Interest Paid}_{Prep.}\\&=\frac{P}{1-(1+\frac{i}{12})^{-n}}[(n-z)(\frac{i}{12})-\frac{i}{i'}-(1-(1+\frac{i}{12})^{m-n-1}-\frac{i}{i'})(1+\frac{i'}{12})^{z-m+1}].\end{split}\end{equation*}](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-b6dbaa947a96b0d45784a96a89ea958e_l3.png)
The Total Interest Loss Proportion is thus given by:
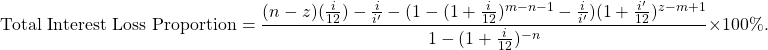
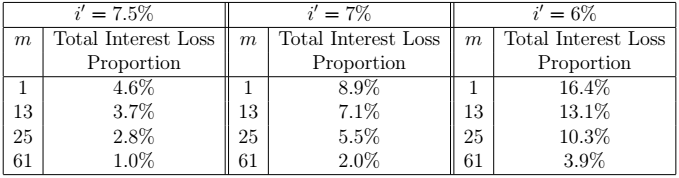
The next two tables give the Total Interest Loss Proportion for the 10-year ![]() loan and the 20-year
loan and the 20-year ![]() loan respectively, for different values of
loan respectively, for different values of ![]() and
and ![]() .
.
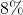 Loan for various
Loan for various 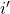 and
and 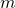 values
values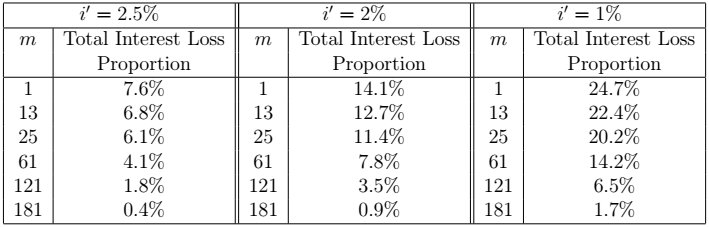
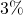 Loan for various
Loan for various 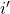 and
and 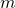 values
valuesPrepayment on a Portfolio of Loans resulting from a decrease in the interest rates
Suppose that we have a portfolio of ![]() loans. A loan is initiated at time
loans. A loan is initiated at time ![]() (that is the drawdown is at
(that is the drawdown is at ![]() and the first repayment starts at
and the first repayment starts at ![]() ), has principal
), has principal ![]() , yearly interest rate
, yearly interest rate ![]() , and duration
, and duration ![]() , for
, for ![]() . Suppose that the time is a non-negative integer, set
. Suppose that the time is a non-negative integer, set ![]() and let the time now be
and let the time now be ![]() . Suppose that at the time now,
. Suppose that at the time now, ![]() , the interest rates change from
, the interest rates change from ![]() to
to ![]() ,
, ![]() . Hence prepayments starts with the repayments at time
. Hence prepayments starts with the repayments at time ![]() . We would like to know the outstanding principal of the whole portfolio at each time
. We would like to know the outstanding principal of the whole portfolio at each time ![]() from
from ![]() onwards, given that prepayment is present and compare it to that when prepayment is not present.
onwards, given that prepayment is present and compare it to that when prepayment is not present.
The outstanding principal of the whole portfolio ![]() at time
at time ![]() for
for ![]() , in the case where prepayment is not present is given by Equation (3). On the other hand, the outstanding principal of the whole portfolio
, in the case where prepayment is not present is given by Equation (3). On the other hand, the outstanding principal of the whole portfolio ![]() for
for ![]() in the case when the prepayments start at
in the case when the prepayments start at ![]() , due to a decrease in the interest rates at time
, due to a decrease in the interest rates at time ![]() , is given by:
, is given by:
(7) 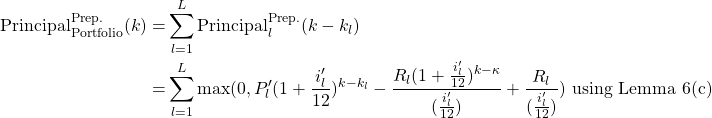
where ![]() is the outstanding principal of the
is the outstanding principal of the ![]() loan at time
loan at time ![]() given that the interest rate decreases to
given that the interest rate decreases to ![]() at the
at the ![]() repayment time, and
repayment time, and ![]() .
.
The prepaid amount and the prepayment rate of the portfolio at time ![]() are obtained by substituting Equation (7) in Equations (5) and (6) respectively.
are obtained by substituting Equation (7) in Equations (5) and (6) respectively.
Recall that the expected inflow of interest income at month ![]() (that is the case in which prepayment is not present) is given by:
(that is the case in which prepayment is not present) is given by:
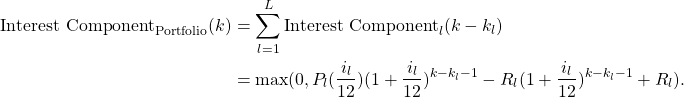
The actual inflow of interest income at month ![]() , given a decrease in the interest rates is given by the equation:
, given a decrease in the interest rates is given by the equation:
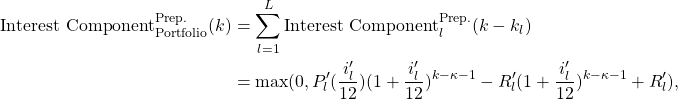
for ![]() , where
, where ![]() is the interest component in the
is the interest component in the ![]() month of loan
month of loan ![]() , given that interest rate decreases to
, given that interest rate decreases to ![]() at month
at month ![]() and
and ![]() .
.
The Interest Loss on the whole portfolio at time ![]() , for
, for ![]() is the difference between
is the difference between ![]() and
and ![]() .
.
Consider the following example. Suppose we have a portfolio made up of three loans as characterised in the next table.

Let the time now be ![]() and at the time now, the interest rates of all the loans in the portfolio and decreased by
and at the time now, the interest rates of all the loans in the portfolio and decreased by ![]() . Hence the interest rate of Loan 1 changes to
. Hence the interest rate of Loan 1 changes to ![]() (
(![]() ), the interest rate of Loan 2 changes to
), the interest rate of Loan 2 changes to ![]() (
(![]() ) and the interest rate of Loan 3 changes to
) and the interest rate of Loan 3 changes to ![]() (
(![]() ). This will lead to prepayments from time
). This will lead to prepayments from time ![]() onwards.
onwards.
The next table gives some results derived from Equations (3), (7), (5) and (6). Note that the month numbers are chosen at an interval of 12. So the row corresponding to 84 shows the state of the portfolio after a year of prepayments, the row corresponding to 96 shows the state of the portfolio after two years of prepayments and so on.
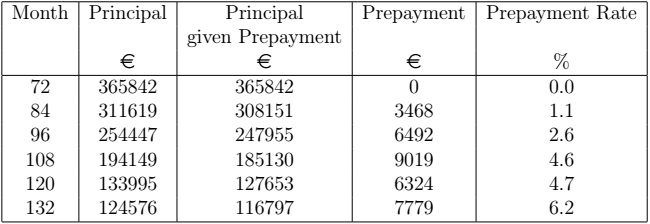
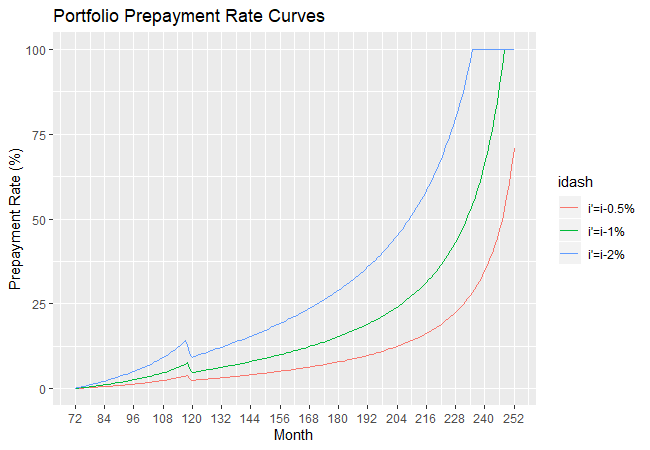
The next figure shows the portfolio prepayment rate curves when the interest rates are decreased by ![]() ,
, ![]() and
and ![]() .
.
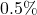 ,
, 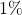 , and
, and 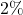
Consider the prepayment rate curve resulting from a decrease of ![]() in the interest rates. This reaches a local maximum of 7.6\% at month 118, which is the month before both Loan 1 and Loan 3 are repaid in full. It reaches a local minimum at month 120, by which time the outstanding principal of both Loan 1 and Loan 3 have reached an outstanding principal of 0 according to their respective repayment schedules (excluding prepayment). From that month onwards, the prepayment rate curve keeps on increasing to reach 100\% at which time Loan 3 is repaid in full. Note that since the repayment schedule (excluding prepayment) is independent of
in the interest rates. This reaches a local maximum of 7.6\% at month 118, which is the month before both Loan 1 and Loan 3 are repaid in full. It reaches a local minimum at month 120, by which time the outstanding principal of both Loan 1 and Loan 3 have reached an outstanding principal of 0 according to their respective repayment schedules (excluding prepayment). From that month onwards, the prepayment rate curve keeps on increasing to reach 100\% at which time Loan 3 is repaid in full. Note that since the repayment schedule (excluding prepayment) is independent of ![]() , all the three prepayment rate curves reach a local minimum at month 120.
, all the three prepayment rate curves reach a local minimum at month 120.
One could then derive the inflow of portfolio principal during the next five years, shown in the next table. The expected principal inflow is the sum of the capital portion of each repayment during a particular year, while the actual principal inflow is the sum of the capital portion of each repayment during a particular year given that prepayment is present.
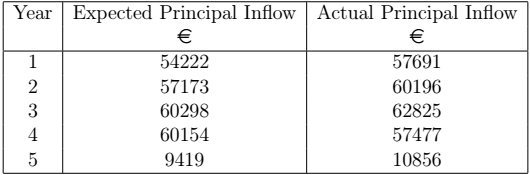
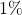
The next figure displays the extension of the data presented in the above table to 20 years.
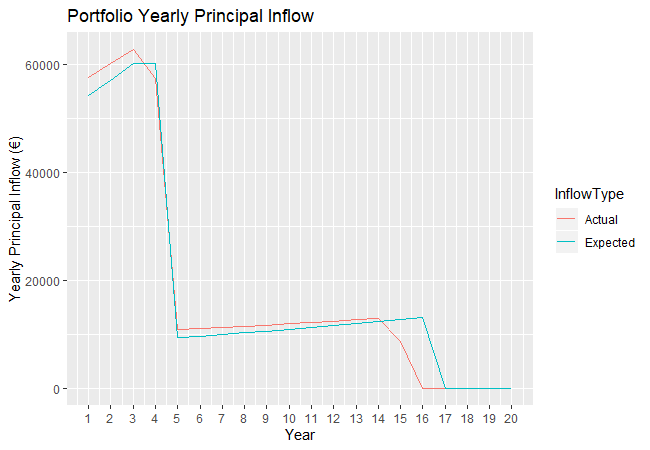
Next we consider the expected and actual inflow of interest income. The next figure shows the monthly inflow of expected interest income and the actual interest income given the increase a decrease in the interest rates by ![]() ,
, ![]() and
and ![]() .
.

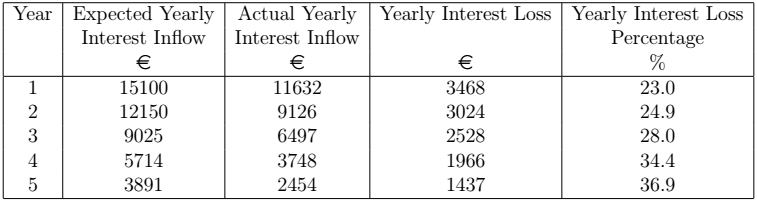
These monthly figures can be group in order to obtain the yearly expected and actual inflow of interest income. The next table gives the annual inflow of interest income, both expected and actual, during the next five years for the case when the interest rates are decreased by ![]() . Their difference results in the loss of interest income over a yearly basis. The loss can be expressed a percentage by computing the fraction of yearly interest loss over the expected yearly inflow of interest income.
. Their difference results in the loss of interest income over a yearly basis. The loss can be expressed a percentage by computing the fraction of yearly interest loss over the expected yearly inflow of interest income.
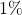
Conclusion
We studied the effects of prepayments on a loan, resulting from two different scenarios. The first scenario is when the repayments are increased by some factor from one time point onwards. The second scenario is when the interest rate of the loan is decreased at some time point whilst the monthly repayment amount remains unchanged. Both instances result in prepayment on the loan due to premature repayment of the principal. For each scenario, we found closed formulae for the actual duration of the loan and the prepayment rate of the loan at each month. Moreover a formula is obtained to quantify the interest income lost due to the prepayment.
All of this was combined in order to study a portfolio of loans. We obtain the prepayment rate of the whole portfolio and constructed prepayment rate graphs. We computed the actual outstanding (combined portfolio) principal given the presence of prepayment and compared it to the expected outstanding principal. This is useful for the asset-liability management of the lending institution. The actual interest income inflow from the portfolio of loans is also calculated. This can also be used as a risk assessment measure of the future income of the lending institution.