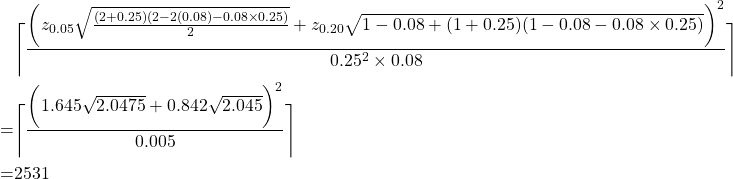How to calculate the sample size for an A/B testing, Including Calculator & Derivation

Introduction

Suppose that we have two treatments A and B representing two different marketing strategies. Treatment A is called the “control” that represents the marketing strategy that is already in place and Treatment B is called the “variation” that represents a newly-developed marketing strategy. We are going to compare the two different marketing strategies A and B by comparing the conversion rate associated with each strategy. The conversion rate is equal to the number of purchases over the number of visiting customers. For example, when considering an e-commerce website, the conversion rate for treatment A, is found by calculating how much of the number of website visitors who view the website designed according to marketing strategy A, purchase the product. A higher conversion rate is an indication of a good marketing strategy whereas a low conversion rate is an indication of a poor marketing strategy. In A/B testing, we decide whether or not there is a significant difference between the two strategies, and if there exists a significant difference, we find which strategy is superior and quantify such a significant difference. The main statistical tool for A/B testing is Hypothesis Testing, and in particular when conversion rates are involved, we are using the test of proportions.

In this article we will first provide a calculator that calculates the required sample size needed before the A/B test is conducted that ensures a proper comparison between the two treatments. The formula for the required sample size is then shown together with a full mathematical description and derivation of the A/B test and the associated sample size equation.

Sample Size Calculator for A/B Testing

Control Conversion Rate ( $\hat{p}_A$ in %):

Minimum Detectible Effect (in %):

Confidence Level (1- $\alpha$ ):

Power (1- $\beta$ ):

Sample Size per Variation:

The control conversion rate is the conversion rate associated with the marketing strategy already in place.
The confidence level is the probability of correctly stating that the variation is not a better alternative to the marketing strategy already in place.
The power is the probability of correctly stating that the variation is indeed a better alternative to the marketing strategy already in place.
The minimum detectible effect is the value 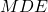$MDE$ such that the test can identify a relative increase of 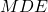$MDE$ or more from the conversion rate of A to the conversion rate of B, with a confidence level of at least 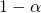$1-\alpha$ and a power of at least $1-\beta$ .

For example, suppose that the conversion rate associated with the marketing strategy already in place is 8%, that is $\hat{p}_A$ is 8%. Suppose that the minimum detectible effect is 25%, the confidence level is 95% and the power is 80%. The required sample size for the variant B is 2513. Thus if we have a sample of 2513 customers for variant B, we can perform the A/B test and be able to correctly state that variant B offers no better alternative to the control A with probability 95%, or else correctly state that variant B offers a better alternative to A with probability of at least 80%, when the percentage change from the conversion rate of A to the conversion rate of B is at least 25%.

Required Sample Size Formula for A/B Testing

The minimum sample size for the variation B given a control conversion rate $\hat{p}_A$ , a minimum detectible effect $MDE$ , that ensures a confidence level $1-\alpha$ and power of at least $1-\beta$ is:

$\Bigg\lceil\frac{\bigg(z_{\alpha}\sqrt{\frac{(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE)}\bigg)^2}{MDE^2 \hat{p}_A}\Bigg\rceil$

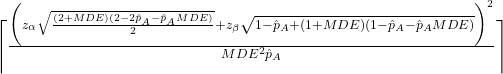
Thus, if the percentage change from $p_A$ to $p_B$ is $MDE$ or more, and we have such a sample size for variation B, we can perform the A/B Testing with a probability of a Type 1 error of at most $\alpha$ and a probability of a Type 2 error of at most $\beta$ . The following section gives the mathematical derivation of the sample size equation.

Mathematical Derivation of the Sample Size

Let $p_A$ be population proportion (i.e. the conversion rate) for the control A and let $p_B$ be population proportion (i.e. the conversion rate) for treatment B. We will use the one-tailed set of hypothesis. Thus the hypotheses for the test of proportions are:

$H_0:\ p_A-p_B=0$

$H_1:\ p_A-p_B< 0$

The control A is the marketing strategy that is currently in place. If the marketing strategy B is better, that is $p_B>p_A$ , then the alternative hypothesis $H_1$ ( $p_A-p_B<0$ ) will be true. If the marketing strategy B is worse or equally as effective as marketing strategy A, then B is disregarded.

In practice the true values of $p_A$ and $p_B$ are unknown and in statistics we use the sample proportions $\hat{p}_A$ and $\hat{p}_B$ to derive results on the two population parameters $p_A$ and $p_B$ and thus we are able to choose one of the two hypotheses. In hypotheses testing we can make two types of errors. The first one is when we accept $H_0$ when in reality $H_0$ is not true. This is known as a Type 1 error. The second one is when we reject $H_0$ when in reality $H_0$ is true. The probability of making a Type 1 error is $\alpha$ and the probability of making a Type 2 error is $\beta$ . We are after an appropriate sample size that ensures that both $\alpha$ and $\beta$ are fixed to certain pre-defined values. A common value for $\alpha$ is 0.05 (5%), whereas a common value for $\beta$ is 0.20 (20%). Thus, in such a case, we will be finding a sample size that ensures that the probability of a Type 1 error is 5% whereas the probability of a Type 2 error is no more than 20%.

Let $n_A$ and $n_B$ be the sample sizes for control A and variation B respectively. Recall, that from probability theory, the sampling distribution of the difference $\hat{p}_A-\hat{p}_B$ is given by:

$\hat{p}_A-\hat{p}_B\sim\mathcal{N}(p_A-p_B,\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B})$

Therefore,

$Z=\frac{\hat{p}_A-\hat{p}_B-(p_A-p_B)}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}}\sim\mathcal{N}(0,1)$

We are going to fix the probability of a Type 1 error to be equal to $\alpha$ . Hence:

$\begin{equation*} \begin{split} \mathbb{P}[H_0\mbox{ is rejected}|H_0\mbox{ is true}]&=\alpha\\ \mathbb{P}[H_0\mbox{ is accepted}|H_0\mbox{ is true}]&=1-\alpha\\ \mathbb{P}[ Z\leq z_{\alpha}|H_0\mbox{ is true}]&=1-\alpha\mbox{ (where }\alpha\mbox{ is the critical value corresponding to a cumulative probability of }1-\alpha)\\ \mathbb{P}[ \frac{\hat{p}_A-\hat{p}_B-(p_A-p_B)}{\sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}} \leq z_{\alpha}|H_0\mbox{ is true}]&=1-\alpha\\ \mathbb{P}[\frac{\hat{p}_A-\hat{p}_B-0}{\sqrt{P(1-P)(\frac{1}{n_A}+\frac{1}{n_B})}} \leq z_{\alpha}]&=1-\alpha\mbox{ (where }P\mbox{ is the pooled sample proportion }\frac{n_A \hat{p}_A+n_B \hat{p}_B}{n_A+n_B})\\ \mathbb{P}[\hat{p}_A-\hat{p}_B \leq z_{\alpha}\sqrt{P(1-P)(\frac{1}{n_A}+\frac{1}{n_B})}]&=1-\alpha \end{split} \end{equation*}$

If we assume that $n_A=n_B$ , the pooled sample proportion $P$ reduces to $\frac{\hat{p}_A+\hat{p}_B}{2}$ and the $(1-\alpha)$ confidence interval reduces to:

$\begin{equation*} \begin{split} \mathbb{P}[\hat{p}_A-\hat{p}_B \leq z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}]&=1-\alpha \end{split} \end{equation*}$

Now let us consder the probability of a Type 2 error associated with the alternate hypothesis $H_1:\ p_A-p_B< 0$ , in particular with the value $\lambda=p_A-p_B$ . We want the probability of a Type 2 error to be at most $\beta$ . Therefore:

$\begin{equation*} \begin{split} \mathbb{P}[H_0\mbox{ is accepted}|H_1\mbox{ is true}]&\leq\beta\\ \mathbb{P}[H_0\mbox{ is rejected}|H_1\mbox{ is true}]&\geq 1-\beta\\ \mathbb{P}[\hat{p}_A-\hat{p}_B>z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}|H_1\mbox{ is true}]&\geq 1-\beta\\ \mathbb{P}[\frac{\hat{p}_A-\hat{p}_B-\lambda}{\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}}>\frac{z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}-\lambda}{\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}}|H_1\mbox{ is true}]&\geq 1-\beta\\ \mathbb{P}[Z>\frac{z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}-\lambda}{\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}}]&\geq 1-\beta \end{split} \end{equation*}$

For such an inequality to hold, we have:

$\begin{equation*} \begin{split} \frac{z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}-\lambda}{\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}}&\leq -z_{\beta}\\ z_{\alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}-\lambda&\leq -z_{\beta}\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}\\ z_{alpha}\sqrt{\frac{\hat{p}_A+\hat{p}_B}{n_B}(1-\frac{\hat{p}_A+\hat{p}_B}{2})}+z_{\beta}\sqrt{\frac{\hat{p}_A(1-\hat{p}_A)}{n_A}+\frac{\hat{p}_B(1-\hat{p}_B)}{n_B}}&\leq \lambda\\ \frac{1}{\sqrt{n_B}}\bigg(z_{\alpha}\sqrt{(\hat{p}_A+\hat{p}_B)(1-\frac{\hat{p}_A+\hat{p}_B}{2})}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A)+\hat{p}_B(1-\hat{p}_B)}\bigg)&\leq \lambda\\ n_B&\geq \frac{\bigg(z_{\alpha}\sqrt{(\hat{p}_A+\hat{p}_B)(1-\frac{\hat{p}_A+\hat{p}_B}{2})}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A)+\hat{p}_B(1-\hat{p}_B)}\bigg)^2}{\lambda^2} \end{split} \end{equation*}$

Now since the control A is the market strategy already in place, we assume that we would have a value for $\hat{p}_A$ in hand. In fact $\hat{p}_A$ is the control conversion rate which is one of the inputs of the sample size calculator. We will express $p_B$ in terms of $p_A$ as follows:

$p_B=(1+MDE)p_A$ ,

and $\hat{p}_B$ in terms of $\hat{p}_A$ as follows:

$\hat{p}_B=(1+MDE)\hat{p}_A$ ,

where $MDE$ stands for the minimum detectable effect, and is the minimum percentage increase from $p_A$ and $p_B$ , that results in a test having confidence level $1-\alpha$ and power at least $1-\beta$ .

Therefore,

$\begin{equation*} \begin{split} n_B&\geq \frac{\bigg(z_{\alpha}\sqrt{(\hat{p}_A+\hat{p}_B)(1-\frac{\hat{p}_A+\hat{p}_B}{2})}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A)+\hat{p}_B(1-\hat{p}_B)}\bigg)^2}{\lambda^2}\\ &=\frac{\bigg(z_{\alpha}\sqrt{(\hat{p}_A+(1+MDE)\hat{p}_A)(1-\frac{\hat{p}_A+(1+MDE)\hat{p}_A}{2})}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A)+(1+MDE)\hat{p}_A(1-(1+MDE)\hat{p}_A)}\bigg)^2}{(p_A-(1+MDE)p_A)^2}\\ &=\frac{\bigg(z_{\alpha}\sqrt{\frac{\hat{p}_A(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE))}\bigg)^2}{(-MDE p_A)^2}\\ &=\frac{\bigg(z_{\alpha}\sqrt{\frac{\hat{p}_A(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE))}\bigg)^2}{MDE^2 p_A^2}\\ &\simeq\frac{\bigg(z_{\alpha}\sqrt{\frac{\hat{p}_A(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{\hat{p}_A(1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE))}\bigg)^2}{MDE^2 \hat{p}_A^2}\mbox{(since we are using }\hat{p}_A\mbox{ as an estimate of }p_A)\\ &=\frac{\bigg(z_{\alpha}\sqrt{\frac{(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE)}\bigg)^2}{MDE^2 \hat{p}_A}\\ \end{split} \end{equation*}$

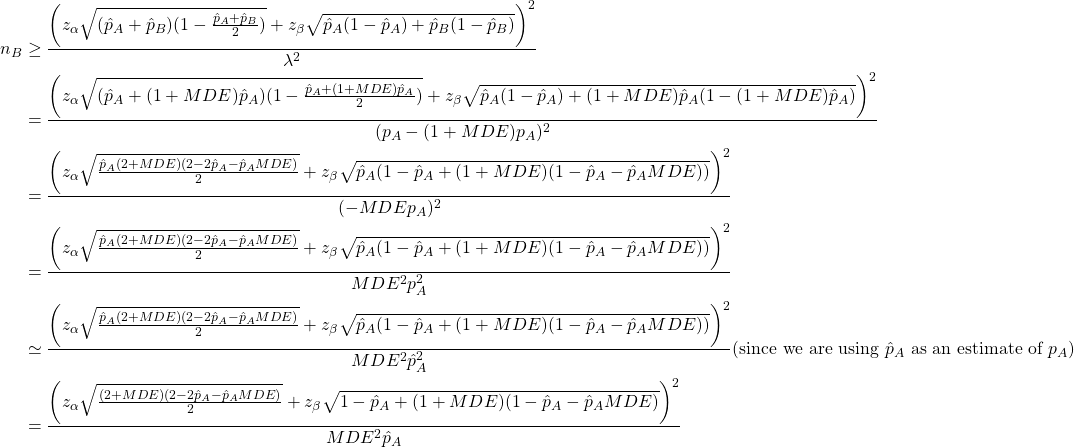
Thus the minimum sample size for the variation B given a control conversion rate $\hat{p}_A$ , a minimum detectible effect $MDE$ , confidence level $1-\alpha$ and power at least $1-\beta$ is:

$\Bigg\lceil\frac{\bigg(z_{\alpha}\sqrt{\frac{(2+MDE)(2-2\hat{p}_A-\hat{p}_A MDE)}{2}}+z_{\beta}\sqrt{1-\hat{p}_A+(1+MDE)(1-\hat{p}_A-\hat{p}_A MDE)}\bigg)^2}{MDE^2 \hat{p}_A}\Bigg\rceil$

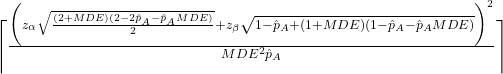
Worked Example

Suppose that the conversion rate associated with the marketing strategy already in place is 8%, that is $\hat{p}_A$ is 8%. Suppose that if the percentage change from the conversion rate of strategy A to the conversion rate of strategy B, is 25% or more, we can perform an A/B testing with confidence level of at least 95% and power 80%. Thus $\alpha=0.05$ , $\beta=0.20$ and $MDE$ is 25%. The required minimum sample size is:

$\begin{equation*} \begin{split} &\Bigg\lceil\frac{\bigg(z_{0.05}\sqrt{\frac{(2+0.25)(2-2(0.08)-0.08\times 0.25)}{2}}+z_{0.20}\sqrt{1-0.08+(1+0.25)(1-0.08-0.08\times 0.25)}\bigg)^2}{0.25^2 \times 0.08}\Bigg\rceil\\ =&\Bigg\lceil\frac{\bigg(1.645\sqrt{2.0475}+0.842\sqrt{2.045}\bigg)^2}{0.005}\Bigg\rceil\\ =&2531 \end{split} \end{equation*}$