How many non isomorphic groups of order 4 are there?
We will show that there are exactly two non isomorphic groups of order 4, namely the cyclic group of order 4, denoted by ![]() and the Klein four-group, denoted by
and the Klein four-group, denoted by ![]() .
.
Recall that:
![]() , where
, where ![]() .
.
and
![]() where
where ![]() and
and ![]() ,
, ![]() and
and ![]() .
.
Prove that there are exactly two non isomorphic groups of order 4, namely the cyclic group of order 4 and the Klein four-group.
Let ![]() be a group of order 4. By Lagrange’s Theorem, it follows that the order of any element
be a group of order 4. By Lagrange’s Theorem, it follows that the order of any element ![]() of
of ![]() divides the order of the group
divides the order of the group ![]() .
.
Hence the order of the elements of ![]() must divide 4.
must divide 4.
Hence the order of the elements of ![]() are 1, 2 or 4.
are 1, 2 or 4.
The group ![]() has 4 elements. One and only one element has order 1, namely, the identity element (which is unique). Hence the remaining three elements must have order 2 or 4.
has 4 elements. One and only one element has order 1, namely, the identity element (which is unique). Hence the remaining three elements must have order 2 or 4.
Consider the following two cases:
Case 1: The group ![]() has an element of order 4
has an element of order 4
Case 2: The group ![]() has no element of order 4
has no element of order 4
Case 1: The group 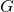 has an element of order 4
has an element of order 4
Let ![]() have order 4. Hence, by definition of order,
have order 4. Hence, by definition of order, ![]() where
where ![]() ,
, ![]() and
and ![]() .
.
Since ![]() is a group, it contains the identity element, hence
is a group, it contains the identity element, hence ![]() . We already know that
. We already know that ![]() , and by closure
, and by closure ![]() .
.
Since ![]() has order 4 and
has order 4 and ![]() , then
, then ![]() which is the cyclic group
which is the cyclic group ![]() .
.
Case 2: The group 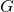 has no element of order 4
has no element of order 4
Let ![]() . Since
. Since ![]() has no element of order 4, it must follow that
has no element of order 4, it must follow that ![]() and
and ![]() have order 2. Therfore,
have order 2. Therfore, ![]() .
.
Let us draw the Cayley table of this group.
Using the fact that the identity element leaves every element unchanged and that ![]() , we have:
, we have:
![Rendered by QuickLaTeX.com \[\begin{array}{c| c c c c} & e & x & y & z \\ \hline e & e & x & y & z \\ x & x & e & & \\ y & y & & e & \\z & z & & & e\end{array}\]](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-6cd121811132291b33cbf91a1599747d_l3.png)
By the axioms of groups, every element of the group must be included exactly once in every row and column of the Cayley table. Hence in row 2 column 3 one cannot put ![]() (because it is already used in row 2 column 1) and one cannot put
(because it is already used in row 2 column 1) and one cannot put ![]() because it is already used in row 1 column 3. Hence it must be
because it is already used in row 1 column 3. Hence it must be ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{c| c c c c} & e & x & y & z \\ \hline e & e & x & y & z \\ x & x & e & z & \\ y & y & & e & \\z & z & & & e\end{array}\]](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-56e9d968de5b2d6219b1d7033c2e40ff_l3.png)
This procedure is repeated and it follows that the Cayley table can only be filled up in the following unique way.
![Rendered by QuickLaTeX.com \[\begin{array}{c| c c c c} & e & x & y & z \\ \hline e & e & x & y & z \\ x & x & e & z & y \\ y & y & z & e & x \\z & z & y & x & e\end{array}\]](https://datasciencegenie.com/wp-content/ql-cache/quicklatex.com-068918f1c1c925c39a3f5738729cc350_l3.png)
Therefore ![]() ,
, ![]() and
and ![]() . This is thus the Klein four-group.
. This is thus the Klein four-group.
Hence the only two groups which have order 4 are the cyclic group and the Klein-four group, and their structure is different, hence they are non-isomorphic. ![]()