Theorem: Let 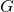 be a simple graph with
be a simple graph with 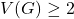 , such that both
, such that both 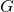 and its complement
and its complement 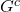 are connected. Then
are connected. Then 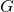 (and its complement
(and its complement 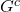 ) has an induced
) has an induced 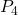 .
.
Proof: First of all note that since the complement of ![]() is still
is still ![]() . Then
. Then ![]() has an induced
has an induced ![]() if and only if
if and only if ![]() has an induced
has an induced ![]() . Similarly,
. Similarly, ![]() has no induced
has no induced ![]() if and only if
if and only if ![]() has no induced
has no induced ![]() .
.
Suppose for contradiction that the theorem statement is false. Suppose that there exists a simple graph ![]() on at least 2 vertices, such that
on at least 2 vertices, such that ![]() (and
(and ![]() ) has no induced
) has no induced ![]() . Let us find a minimal counter example, i.e., a graph
. Let us find a minimal counter example, i.e., a graph ![]() with the minimum possible number of vertices, which is connected, its complement
with the minimum possible number of vertices, which is connected, its complement ![]() connected and has no induced
connected and has no induced ![]() .
.
There are no such graphs on 2 vertices, on 3 vertices and on 4 vertices.
Hence the minimal counterexample ![]() must have at least 5 vertices.
must have at least 5 vertices.
Let ![]() . Consider the subgraph
. Consider the subgraph ![]() . Since
. Since ![]() has no induced
has no induced ![]() and
and ![]() is an induced subgraph of
is an induced subgraph of ![]() , then
, then ![]() also has no induced
also has no induced ![]() . Since
. Since ![]() is a minimal counterexample,
is a minimal counterexample, ![]() (which has less vertices than
(which has less vertices than ![]() ) or its complement must be disconnected.
) or its complement must be disconnected.
W.l.o.g. assume that ![]() is disconnected. Let
is disconnected. Let ![]() be a component of
be a component of ![]() . Since
. Since ![]() is connected, then
is connected, then ![]() is adjacent to at least one vertex of
is adjacent to at least one vertex of ![]() and one vertex of
and one vertex of ![]() . Let us name these two vertices as
. Let us name these two vertices as ![]() and
and ![]() respectively. Moreover, since
respectively. Moreover, since ![]() and
and ![]() are both connected,
are both connected, ![]() is not a dominating vertex. Hence there exists a vertex
is not a dominating vertex. Hence there exists a vertex ![]() in
in ![]() or
or ![]() which is not adjacent to
which is not adjacent to ![]() . W.l.o.g. let us assume that
. W.l.o.g. let us assume that ![]() is in
is in ![]() .
.
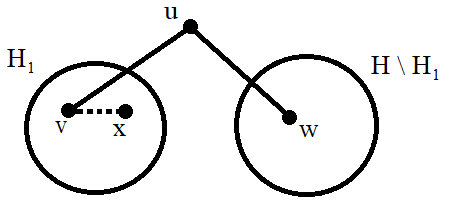
Consider the shortest path ![]() from
from ![]() to
to ![]() , where
, where ![]() (any path from a vertex of
(any path from a vertex of ![]() to a vertex of
to a vertex of ![]() must pass from
must pass from ![]() ) and
) and ![]() . Consider the induced subgraph
. Consider the induced subgraph ![]() . Since
. Since ![]() is a shortest path, we have
is a shortest path, we have ![]() ,
, ![]() and
and ![]() . Thus
. Thus ![]() is an induced
is an induced ![]() . This gives a contradiction. Hence the result follows.
. This gives a contradiction. Hence the result follows. ![]()